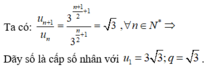Các câu hỏi tương tự
Cho dãy số
(
u
n
)
:
u
1
0
u
n
+
1
...
Đọc tiếp
Cho dãy số ( u n ) : u 1 = 0 u n + 1 = 2 u n + 3 u n + 4 v ớ i n ≥ 1
a) Lập dãy số ( x n ) với x n = u n - 1 u n + 3 . Chứng minh dãy số là cấp số nhân.
b) Tìm công thức tính x n , u n theo n.
Cho dãy số (Un) xác định bởi U1=-3 và U(n+1)=Un+ n^2 -3n +4, mọi n thuộc N*. Số 1391 là số hạng thứ mấy của dãy ?
Cho dãy số
(
u
n
)
với
u
n
n
2
-
4
n
+
3
a) Viết công thức truy hồi của dãy số;b) Chứng minh dãy số bị chặn dưới;c) Tính tổng n số hạng đầu của dãy đã cho.
Đọc tiếp
Cho dãy số ( u n ) với u n = n 2 - 4 n + 3
a) Viết công thức truy hồi của dãy số;
b) Chứng minh dãy số bị chặn dưới;
c) Tính tổng n số hạng đầu của dãy đã cho.
Cho dãy số \(u_n\)xác định bởi \(\hept{\begin{cases}u_1=\frac{1}{3}\\u_n=\frac{n+1}{3n}.u_n\end{cases}}\)Với mọi \(n\inℕ^∗\)
Tìm số hạng tổng quát của dãy và tìm lim(un)
Cho dãy số (un) với
u
n
3
n
2
+
1
.Tìm công bội của dãy số (un). A.
q
3
2
B.
q
3
C.
q
1
2
D.
q
3
Đọc tiếp
Cho dãy số (un) với u n = 3 n 2 + 1 .Tìm công bội của dãy số (un).
A. q = 3 2
B. q = 3
C. q = 1 2
D. q = 3
Cho dãy số
u
n
với
u
n
4
n
-
1
. Tìm công bội của dãy số (un). A. q0,5 B. q0,25 C. q4 D.q16
Đọc tiếp
Cho dãy số u n với u n = 4 n - 1 . Tìm công bội của dãy số (un).
A. q=0,5
B. q=0,25
C. q=4
D.q=16
Cho dãy số
u
1
1
3
u
n
+
1
...
Đọc tiếp
Cho dãy số u 1 = 1 3 u n + 1 = n + 1 u n 3 n v ớ i n ≥ 1
a) Viết năm số hạng đầu của dãy số.
b) Lập dãy số ( v n ) với v n = u n n . Chứng minh dãy số ( v n ) là cấp số nhân.
c) Tìm công thức tính ( u n ) theo n.
Cho dãy số (Un), với un = 1/1×2+ 1/2×3 + 1/3×4 +...+ 1/n(n+1). Xét tính tăng, giảm và bị chặn của dãy số.
Dãy số
u
n
cho bởi
u
1
3
,
u
n
+
1
1
+
u
n
2
,
n
1...
Đọc tiếp
Dãy số u n cho bởi u 1 = 3 , u n + 1 = 1 + u n 2 , n > 1
a. Viết năm số hạng đầu của dãy số.
b. Dự đoán công thức số hạng tổng quát un và chứng minh công thức đó bằng phương pháp quy nạp.