Question

cho ΔABC, hai đường phân giác của hai góc ngoài đỉnh B và đỉnh C cắt nhau tạiE. chứng minh E thuộc phân giác trong của BAC

Answer 1

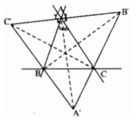
Kẻ EH⊥BC tại H, EM⊥AB tại M, EN⊥AC tại N

Xét ΔBME vuông tại M và ΔBHE vuông tại H có

BE chung

\(\hat{MBE}=\hat{HBE}\)

Do đó: ΔBME=ΔBHE

=>EM=EH(1)

Xét ΔCHE vuông tại H và ΔCNE vuông tại N có

CE chung

\(\hat{HCE}=\hat{NCE}\)

Do đó: ΔCHE=ΔCNE

=>EH=EN(2)

Từ (1),(2) suy ra EM=EN

Xét ΔAME vuông tại M và ΔANE vuông tại N có

AE chung

EM=EN

Do đó: ΔAME=ΔANE

=>\(\hat{MAE}=\hat{NAE}\)

=>AE là phân giác của góc BAC