Question

Cho ΔABC cân tại A.Đường cao AH.Vẽ BK⊥AC(H∈BC,K∈AC)

C/m : \(\dfrac{1}{BK^2}\)=\(\dfrac{1}{BC^2}+\dfrac{1}{4AH^2}\)

Answer 1

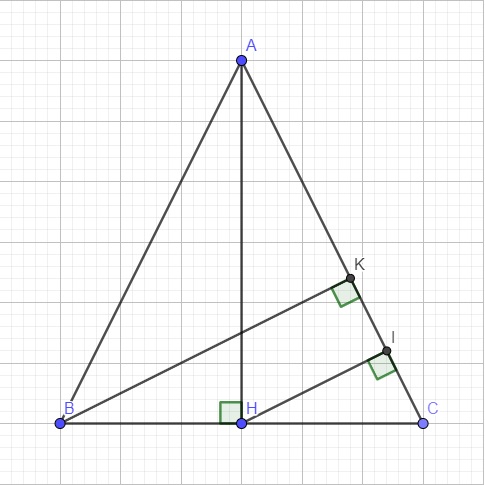
Từ H kẻ \(HI\perp AC\Rightarrow HI||BK\) (cùng vuông góc AC)

Mà tam giác ABC cân tại A \(\Rightarrow H\) là trung điểm BC

\(\Rightarrow HI\) là đường trung bình tam giác BCK

\(\Rightarrow HI=\dfrac{BK}{2}\)

Áp dụng hệ thức lượng trong tam giác vuông AHC với đường cao HI:

\(\dfrac{1}{HI^2}=\dfrac{1}{HC^2}+\dfrac{1}{AH^2}\Leftrightarrow\dfrac{1}{\left(\dfrac{BK}{2}\right)^2}=\dfrac{1}{\left(\dfrac{BC}{2}\right)^2}+\dfrac{1}{AH^2}\)

\(\Leftrightarrow\dfrac{4}{BK^2}=\dfrac{4}{BC^2}+\dfrac{1}{AH^2}\)

\(\Leftrightarrow\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{4AH^2}\)

Answer 2