Chọn đáp án A
Phương pháp
u 5 = S 5 - S 4
Cách giải
Ta có:
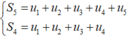
![]()
Chọn đáp án A
Phương pháp
u 5 = S 5 - S 4
Cách giải
Ta có:
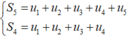
![]()
Cho cấp số nhân u n có tổng n số hạng đầu tiên là S n = 6 n - 1 . Tìm số hạng thứ năm của cấp số nhân đã cho
A. 120005
B. 6840
C. 7775
D. 6480
Cho cấp số cộng (un) có số hạng đầu là u1 = 1 và công sai d = 1. Tìm n sao cho tổng của n số hạng đầu tiên của cấp số cộng đó bằng 3003.
A. n = 79
B. n = 78
C. n = 77
D. n = 80
Ba số phân biệt có tổng 217, là các số hạng liên tiếp của một cấp số nhân, theo thứ tự đó chúng lần lượt là số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng. Biết tổng của n số hạng đầu tiên của cấp số cộng là 820, khi đó n bằng
A. 21
B. 42
C.20
D. 17
Cho cấp số cộng u n có tổng của n số hạng đầu tiên được tính bởi công thức S n = 4 n – n ^ 2. Gọi M là tổng của số hạng đầu tiên và công sai của cấp số cộng. Khi đó:
A. M = -1
B. M = 1
C. M = 4
D. M = 7
Cho cấp số cộng có tổng n số hạng đầu là S n = 3 n 2 + 4 n , n ∈ ℕ * . Giá trị của số hạng thứ 10 của cấp số cộng là
A. u 10 = 67 .
B. u 10 = 61 .
C. u 10 = 59 .
D. u 10 = 55 .
Cho cấp số cộng có tổng của n số hạng đầu tiên được tính bởi công thức Sn = 4n – n2. Gọi M là tổng của số hạng đầu tiên và công sai của cấp số cộng đó. Khi đó :
A. M = 7
B. M = 4
C. M = 2
D. M = 1
Cho cấp số cộng ( u n ) và gọi S n là tổng n số hạng đầu tiên của nó. Biết S 7 = 77 v à S 12 = 192 . Tìm số hạng tổng quát u n của cấp số cộng đó
A. u n = 5 + 4 n .
B. u n = 3 + 2 n .
C. u n = 2 + 3 n .
D. u n = 4 + 5 n .
Cho cấp số cộng ( u n ) có công thức tổng quát là u n = 5 - 2 n , n ∈ ℕ * . Tính tổng 20 số hạng đầu tiên của cấp số cộng.
A. -350
B. 440
C. -320
D. -340