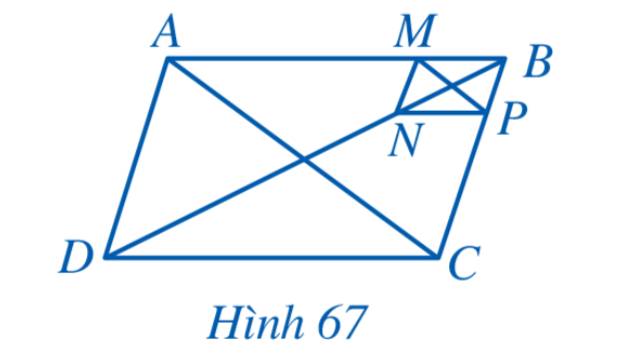
a) Vì ABCD và BMNP là hình bình hành nên \(MN//BP\) và \(AD//BC \Rightarrow MN//AD\)
Xét tam giác ABD có \(AD//MN \Rightarrow \frac{{BM}}{{BA}} = \frac{{BN}}{{BD}}\) (1) (Định lý Thales)
Tương tự ta chứng minh được \(NP//DC \Rightarrow \frac{{BN}}{{BD}} = \frac{{BP}}{{BC}}\)(2)
Từ (1) và (2) ta có \(\frac{{BM}}{{BA}} = \frac{{BP}}{{BC}}\).
b) Ta có \(\frac{{BM}}{{BA}} = \frac{{BP}}{{BC}} \Rightarrow MP//AC\)(Định lý Thales đảo)
\( \Rightarrow \Delta PBM \backsim\Delta CBA\) (c-c-c) (3)
Vì BMNP là hình bình hành nên ta có \(\frac{{PB}}{{MN}} = \frac{{BM}}{{NP}} = \frac{{MP}}{{PM}} = 1\)
\( \Rightarrow \Delta PBM \backsim\Delta MNP\) (c-c-c) (4)
Từ (3) và (4) ta có \(\Delta MNP \backsim\Delta CBA\).