Các câu hỏi tương tự
Tìm tập xác định D của hàm số
y
l
o
g
(
x
2
-
x
-
2
)
(1)
Đọc tiếp
Tìm tập xác định D của hàm số y = l o g ( x 2 - x - 2 ) (1)
Cho hai hàm số
f
(
x
)
l
o
g
2
x
,
g
(
x
)
2
x
. Xét các mệnh đề sau: I. Đồ thị hai hàm số đối xứng với nhau qua đường thẳng y x II. Tập xác định của hai hàm số trên là R III. Đồ thị hai hàm số cắt nhau tại đúng 1 điểm IV. Hai hàm số đều đồng biến trên tập xác định của nó Có bao nhiêu mệnh đề đún...
Đọc tiếp
Cho hai hàm số f ( x ) = l o g 2 x , g ( x ) = 2 x . Xét các mệnh đề sau:
I. Đồ thị hai hàm số đối xứng với nhau qua đường thẳng y = x
II. Tập xác định của hai hàm số trên là R
III. Đồ thị hai hàm số cắt nhau tại đúng 1 điểm
IV. Hai hàm số đều đồng biến trên tập xác định của nó
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 2
B. 3
C. 1
D. 4
Trong bốn hàm số
y
x
+
1
x
+
2
,
y
5
x
+
6
x
2
x
,
y
π
6...
Đọc tiếp
Trong bốn hàm số y = x + 1 x + 2 , y = 5 x + 6 x 2 x , y = π 6 x , y = log 3 x có bao nhiêu hàm số đồng biến trên mỗi khoảng xác định của nó?
A. 1
B. 3
C. 2
D. 4
Tìm tập xác định của hàm số
y
log
(
x
2
-
x
-
2
)
(
1
)
A
.
(
-
∞
;
1
)
∪
(
2
;
+
∞
)
B
.
(
-
∞...
Đọc tiếp
Tìm tập xác định của hàm số y = log ( x 2 - x - 2 ) ( 1 )
A . ( - ∞ ; 1 ) ∪ ( 2 ; + ∞ )
B . ( - ∞ ; 2 )
C . ( 1 ; + ∞ )
D . ( - 1 ; 1 )
Có bao nhiêu hàm số trong các hàm số sau đây đồng biến trên tập xác định của nó:
y
sin
x
,
y
2019
x
,
y
log
2
x
2
+
1
,
y
x
5
+
x
4...
Đọc tiếp
Có bao nhiêu hàm số trong các hàm số sau đây đồng biến trên tập xác định của nó: y = sin x , y = 2019 x , y = log 2 x 2 + 1 , y = x 5 + x 4 - 3 x 2 + 10 x - 3
A. 4
B. 3
C. 1
D. 2
Tìm tập xác định của hàm số
y
log
(
x
2
-
x
-
2
)
A.
(
-
∞
;
-
1
)
∪
(
2
;
+
∞
)
B.
(
-
∞
;
2
)...
Đọc tiếp
Tìm tập xác định của hàm số y = log ( x 2 - x - 2 )
A. ( - ∞ ; - 1 ) ∪ ( 2 ; + ∞ )
B. ( - ∞ ; 2 )
C. ( 1 ; + ∞ )
D. (-1; 1)
trong các hàm số sau hàm số nào đồng biến trên R: A. y= 2x-1/x+2 B. y= -x^3+x^2-5x C. y= x^3+2x+1 D.-x^4-2x^2+3
Cho hàm số yf(x) có đạo hàm liên tục trên R và có đồ thị hàm số yf (x) như hình vẽ bên dưới. Xét hàm số g(x)f(x^2-3) và các mệnh đề sau: I. Hàm số có 3 điểm cực trị. II. Hàm số g(x)đạt cực tiểu tại x0 III. Hàm số g(x) đạt cực đại tại x2 IV. Hàm số g(x) đồng biến trên khoảng (-2;0) V. Hàm số g(x) nghịch biến trên khoảng (-1;1) Có bao nhiêu mệnh đề đúng trong các mệnh đề trên? A.1 B.4 C.3 D.2
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f '(x) như hình vẽ bên dưới. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:
I. Hàm số 
có 3 điểm cực trị.
II. Hàm số g(x)đạt cực tiểu tại x=0
III. Hàm số g(x) đạt cực đại tại x=2
IV. Hàm số g(x) đồng biến trên khoảng (-2;0)
V. Hàm số g(x) nghịch biến trên khoảng (-1;1)
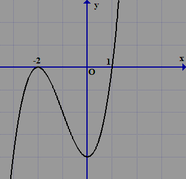
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A.1
B.4
C.3
D.2
Hàm số yf(x) có bảng biến thiên ở bên. Trong các phát biểu dưới đây có bao nhiêu phát biểu đúng? (*): y 3 là tiệm cận ngang (*): Tập xác định
D
ℝ
/
2
(*): Max y 3 (*): Min y -1 (*):
x
C
Đ
2
Đọc tiếp
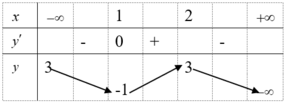
Hàm số y=f(x) có bảng biến thiên ở bên. Trong các phát biểu dưới đây có bao nhiêu phát biểu đúng?
(*): y = 3 là tiệm cận ngang
(*): Tập xác định D = ℝ / 2
(*): Max y = 3 (*): Min y = -1
(*): x C Đ = 2
