Các câu hỏi tương tự
Cho ba điểm A, O, B thẳng hàng theo thứ tự đó, OA a, OB b (a,b cùng đơn vị: cm).Qua A và B vẽ theo thứ tự các tia Ax và By cùng vuông góc với AB và cùng phía với AB. Qua O vẽ hai tia vuông góc với nhau và cắt Ax ở C, By ở D (xem hình 116).Với
C
O
A
^
60
o
cho hình vẽ quay xung quanh AB. Tính tỉ số thể tích các hình do các tam giác AOC và BOD tạo thành.
Đọc tiếp
Cho ba điểm A, O, B thẳng hàng theo thứ tự đó, OA = a, OB = b (a,b cùng đơn vị: cm).
Qua A và B vẽ theo thứ tự các tia Ax và By cùng vuông góc với AB và cùng phía với AB. Qua O vẽ hai tia vuông góc với nhau và cắt Ax ở C, By ở D (xem hình 116).
Với C O A ^ = 60 o cho hình vẽ quay xung quanh AB. Tính tỉ số thể tích các hình do các tam giác AOC và BOD tạo thành.
Cho ba điểm A, O, B thẳng hàng theo thứ tự đó, OA a, OB b (a,b cùng đơn vị: cm).Qua A và B vẽ theo thứ tự các tia Ax và By cùng vuông góc với AB và cùng phía với AB. Qua O vẽ hai tia vuông góc với nhau và cắt Ax ở C, By ở D (xem hình 116).a) Chứng minh AOC và BDO là hai tam giác đồng dạng; từ đó suy ra tích AC.BD không đổi.b) Tính diện tích hình thang ABCD khi
COA
^
60
°
c) Với
COA
^...
Đọc tiếp
Cho ba điểm A, O, B thẳng hàng theo thứ tự đó, OA = a, OB = b (a,b cùng đơn vị: cm).
Qua A và B vẽ theo thứ tự các tia Ax và By cùng vuông góc với AB và cùng phía với AB. Qua O vẽ hai tia vuông góc với nhau và cắt Ax ở C, By ở D (xem hình 116).
a) Chứng minh AOC và BDO là hai tam giác đồng dạng; từ đó suy ra tích AC.BD không đổi.
b) Tính diện tích hình thang ABCD khi COA ^ = 60 °
c) Với COA ^ = 60 ° cho hình vẽ quay xung quanh AB. Tính tỉ số thể tích các hình do các tam giác AOC và BOD tạo thành.
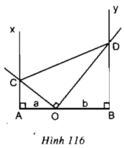
Cho ba điểm A, O, B thẳng hàng theo thứ tự đó, OA = a, OB = b (a,b cùng đơn vị: cm).
Qua A và B vẽ theo thứ tự các tia Ax và By cùng vuông góc với AB và cùng phía với AB. Qua O vẽ hai tia vuông góc với nhau và cắt Ax ở C, By ở D (xem hình 116).
Chứng minh AOC và BDO là hai tam giác đồng dạng; từ đó suy ra tích AC.BD không đổi.
Cho ba điểm A, O, B thẳng hàng, OA a, OB b (a, b cùng đơn vị là cm). Qua A và B vẽ theo thứ tự các tia Ax và By cùng vuông góc với AB. Qua O vẽ hai tia vuông góc với nhau và cắt Ax ở C, By ở Da, Chứng minh các tam giác AOC và BDO đồng dạng. Từ đó suy ra tích AC.BD không đổib, Với
C
O
A
^
60
0...
Đọc tiếp
Cho ba điểm A, O, B thẳng hàng, OA = a, OB = b (a, b cùng đơn vị là cm). Qua A và B vẽ theo thứ tự các tia Ax và By cùng vuông góc với AB. Qua O vẽ hai tia vuông góc với nhau và cắt Ax ở C, By ở D
a, Chứng minh các tam giác AOC và BDO đồng dạng. Từ đó suy ra tích AC.BD không đổi
b, Với C O A ^ = 60 0 , hãy:
i, Tính diện tích hình thang ABCD
ii, Tính tỉ số thể tích các hình do các tam giác AOC và BOD tạo thành khi cho hình vẽ quay xung quanh AB
cho đoạn thẳng AB có độ dài 2a. vẽ về một phía của AB các tia Ax và By vuông góc với AB. qua trung điểm M của AB có hai đường thẳng thay đổi luôn vuông góc với nhau và cắt tia Ax,By theo thứ tự ở C,D. xác định vị trí của các điểm C,D sao cho MCD có diện tích nhỏ nhất
Cho đường tròn (O:R) có đường kính AB và điểm M thuộc đường tròn (M khác A và B). Gọi Ax, By là các tia vuông góc với AB( Ax,By và M cùng thuộc một mặt phẳng bờ AB). Qua điểm M, kẻ tiếp tuyến với đường tròn (O) cắt Ax, By theo thứ tự ở C và D.
a) chứng minh CD=AC+BD
b)OC cắt AM tại H, OD cắt BM tại K. Chứng minh tứ giác OHMK là hình chữ nhật.
c) Chứng minh: AC.BD= R^2
Cho đoạn thẳng AB và điểm M cố định thuộc đường thẳng AB. Vẽ về một phía của AB các tia Ax và By vuông góc với AB. Qua M vẽ hai đường thẳng thay đổi luôn vuông góc với nhau và cắt Ax, By theo thứ tự tại C và D. Xác định vị trí các điểm C và D sao cho diện tích tam giác MCD nhỏ nhất
Cho đoạn thẳng AB và điểm M cố định thuộc đường thẳng AB. Vẽ về một phía của AB các tia Ax và By vuông góc với AB. Qua M vẽ hai đường thẳng thay đổi luôn vuông góc với nhau và cắt Ax, By theo thứ tự tại C và D. Xác định vị trí các điểm C và D sao cho diện tích tam giác MCD nhỏ nhất
Cho nửa đường tròn tâm O có đường kính AB. Gọi Ax, By là các tia vuông góc với AB. Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax và By theo thứ tự ở C và D.
a) xác định vị trí của M để diện tích ACDB nhỏ nhất
b) Từ M kẻ đường thẳng vuông góc với AB tại H. Chứng minh rằng CB đi qua trung điểm I của MH.
Đọc tiếp
Cho nửa đường tròn tâm O có đường kính AB. Gọi Ax, By là các tia vuông góc với AB. Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax và By theo thứ tự ở C và D.
a) xác định vị trí của M để diện tích ACDB nhỏ nhất
b) Từ M kẻ đường thẳng vuông góc với AB tại H. Chứng minh rằng CB đi qua trung điểm I của MH.










