Với ba điểm A, B, C phân biệt.Khi A nằm giữa B, C thì hai vecto A B → ; A C → ngược hướng nên
điều kiện cần và đủ để ba điểm A, B, C thẳng hàng và A nằm giữa B, C là: ∃ k < 0 : A B → = k A C →
Đáp án A
Cho ba điểm phân biệt A, B, C sao cho A B → = k A C → . Để A nằm giữa B và C thì k thỏa mãn điều kiện nào sau đây?
A. k = 1
B. k < 0
C. 0 < k < 1
D. k > 1
Cho ba điểm A, B, C phân biệt sao cho A B → = k A C → . Biết rằng B nằm giữa A và C. Giá trị k thỏa mãn điều kiện nào sau đây?
A. k < 0
B. k = 1
C. 0 < k < 1
D. k > 1
Cho ba điểm A, B, C phân biệt. Điều kiện cần và đủ để ba điểm thẳng hàng là:
A. ∀ M : M A → + M B → + M C → = 0 →
B. ∀ M : M A → + M C → = M B →
C. A C → = A B → + B C →
D. ∃ k ∈ R : A B → = k A C →
Cho bốn điểm phân biệt A, B, C, D. Điều kiện nào trong các đáp án A, B, C, D sau đây là điều kiện cần và đủ để A B → = C D → ?
A. ABCD là hình bình hành.
B. ABDC là hình bình hành.
C. AC = BD
D. AB = CD
Cho tam giác $A B C$ và một điểm $M$ tùy ý. Gọi $A^{\prime}, B^{\prime}, C^{\prime}$ lân lượt là các điêm đôi xứng của $M$ qua các trung điểm $K, I, J$ của các cạnh $B C, C A, A B$.
a) Chứng minh ba đường thẳng $A A^{\prime}, B B^{\prime}, C C^{\prime}$ đồng quy tại một điểm $N$.
b) Chứng minh rằng khi $M$ di động thì đường thẳng $M N$ luôn đi qua trọng tâm $G$ của $\triangle A B C$.
Trong mặt phẳng với hệ tọa độ Oxy cho ba điểm A(0;a) : B( b;0) và C(-b;0) với a; b > 0.Viết phương trình đường tròn (C) tiếp xúc với đường thẳng AB tại B và tiếp xúc với đường thẳng AC tại C.
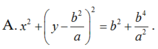
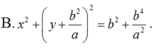
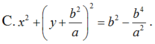
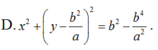
Câu 8: Cho hình bình hành ABCD tâm O. Các vectơ khác 0 ngược hướng với OB là
A. BD OD , . B. BD OD BO , , . C. DB DO , . D. BD BO , .
Câu 9: Cho ba điểm A, B, C thẳng hàng, trong đó điểm B nằm giữa hai điểm A và C. Khi đó các cặp vectơ nào sau đây cùng hướng?
A. CB và AB. B. AB và AC. C. AB và CB . D. BA và BC.
Câu 10: Cho một đa giác 1 2 2019 A A A ... có 2019 cạnh. Số vectơ khác 0 có điểm đầu và điểm cuối được tạo thành từ các đỉnh của đa giác
A. 4074342. B. 8148684. C. 4076361. D. 8152722
GIÚP MÌNH VỚI , MÌNH ĐANG CẦN GẤP!!!!! --- CẢM ƠN!!!!!
Trong mặt phẳng tọa độ Oxy , cho các điểm A( -7; 3), B( 0;1 ), C( -4;2)
a) Chứng minh A, B, C là ba đỉnh của một tam giác
b) Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành. Tìm tọa độ giao điểm hai đường chéo của hình bình hành ABCD
c) Tìm tọa độ điểm E sao cho B là trọng tâm \(\Delta ACE\)
d) Tìm tọa độ điểm M sao cho \(\overrightarrow{AM}=2\overrightarrow{BM}-3\overrightarrow{BC}\)
e) Tìm tọa độ điểm N trên trục hoành sao cho B, C, N thẳng hàng
f) Tìm K( -2, y) để A, B, K thẳng hàng
Giúp mình với, mình đang cần gấp ạ!!!
Trong mặt phẳng Oxy cho A(2;4), B(6;2); C(4;-2)
a) Viết phương trình đường thẳng (h) đi qua A và vuông góc AC
b) Gọi K là giao điểm giữa (h) và trung trực cạnh BC. Tìm tọa độ điểm K. Chứng minh ABHK là hình bình hành
c) Tìm tọa độ điểm D thuộc Oy sao cho tam giác ACD vuông tại C
d) Viết phương trình đường thẳng DC. Tìm tọa độ giao điểm của DC và trục hoành
