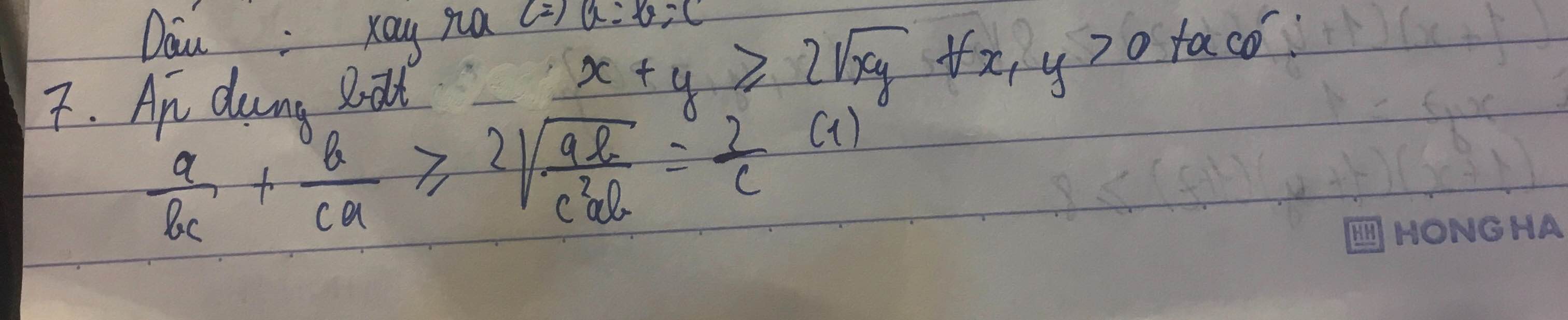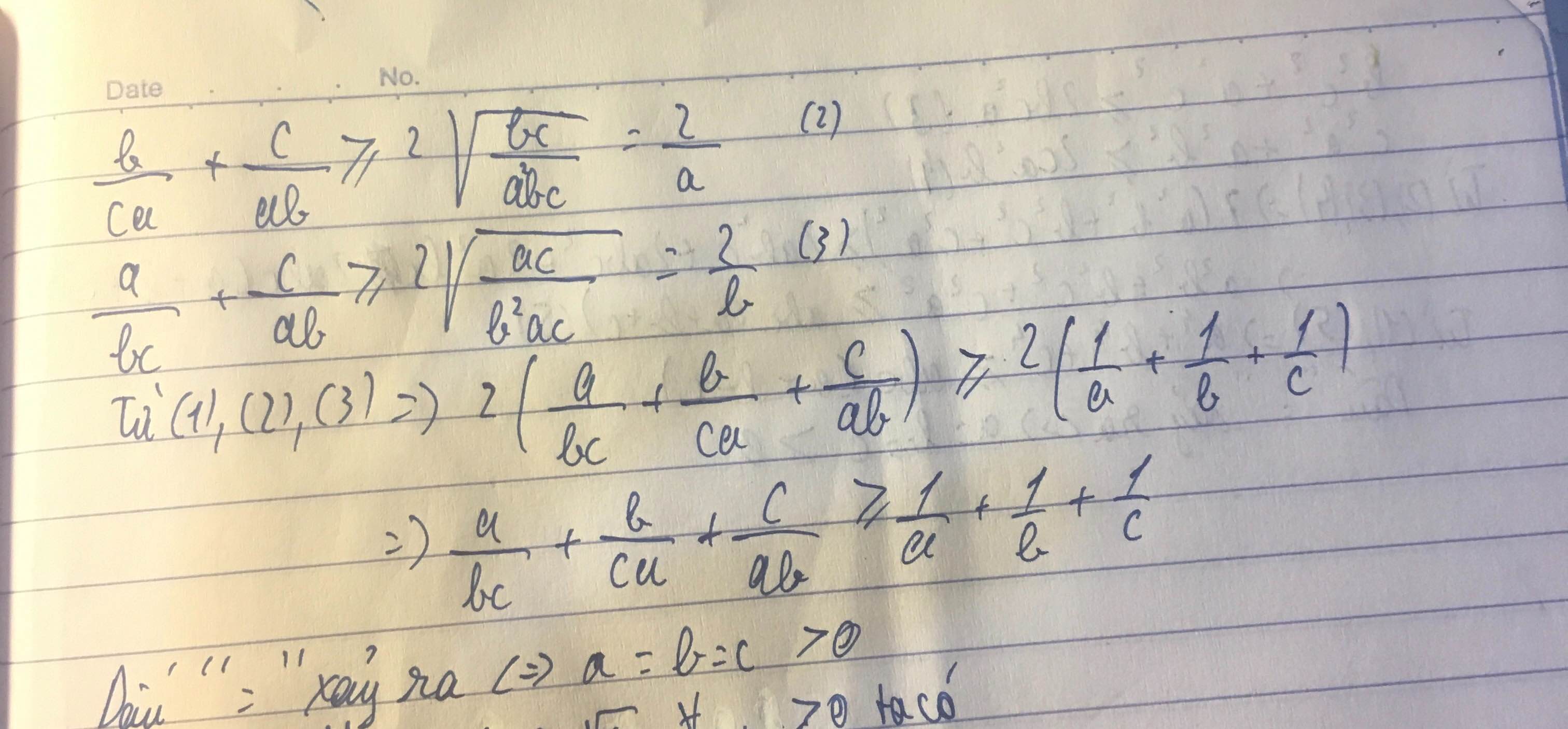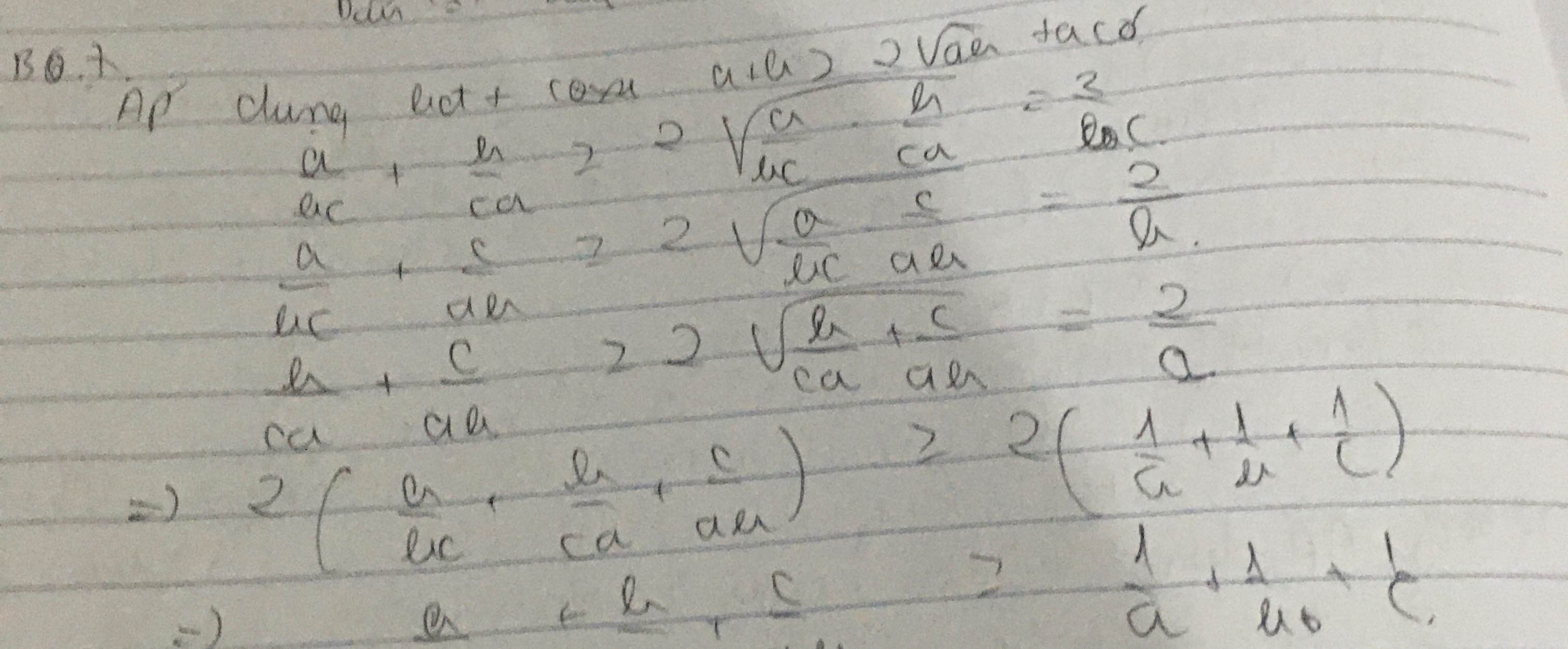Question

Cho \(a,b,c>0\). Chứng minh rằng

     \(\dfrac{a}{bc}+\dfrac{b}{ca}+\dfrac{c}{ab}\ge\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\).

Answer 1

Áp dụng bất đẳng thức cô si ta có, với a,b,c >0

a/bc + b/ac ≥ 2*1/c 

b/ac + c/ab ≥ 2*1/a

a/bc + c/ab ≥ 2*1/b 

Cộng từng vế của 3 bất đẳng thức trên với nhau ta được

2*(a/bc + b/ac + c/ab) ≥ 2(1/a+1/b+1/c) 

<=> đpcm

Answer 2

 

Sử dụng bất đẳng thức Cô si cho hai số dương ta có:

                                   \dfrac{a}{bc}+\dfrac{b}{ca}\ge2\sqrt{\dfrac{a}{bc}.\dfrac{b}{ca}}=\dfrac{2}{b}bca​+cab​≥2bca​.cab​​=b2​

Viết hai bất đẳng thức tương tự rồi cộng theo vế ba bất đẳng thức nhận được rồi chia 2 vế bất đẳng thức cho 2 ta được đpcm.

Answer 3

Answer 4

Answer 5

Answer 6

  

Answer 7

    

Answer 8

  

Answer 9

Áp dụng BĐT Cô-si cho 2 số dương \(\dfrac{a}{bc}\) và \(\dfrac{b}{ca}\) ta có:

\(\dfrac{a}{bc}+\dfrac{b}{ca}\ge2\sqrt{\dfrac{a}{bc}.\dfrac{b}{ca}}=2\sqrt{\dfrac{1}{c^2}}=2.\dfrac{1}{c}\) (1)

Tương tự, ta có: \(\dfrac{b}{ca}+\dfrac{c}{ab}\ge2.\dfrac{1}{a}\) (2) và \(\dfrac{c}{ab}+\dfrac{a}{bc}\ge2.\dfrac{1}{b}\) (3)

Cộng vế theo vế của (1); (2) và (3), ta có:

\(\dfrac{a}{bc}+\dfrac{b}{ca}+\dfrac{b}{ca}+\dfrac{c}{ab}+\dfrac{c}{ab}+\dfrac{a}{bc}\ge2.\dfrac{1}{a}+2.\dfrac{1}{b}+2.\dfrac{1}{c}\)

\(\Leftrightarrow2\left(\dfrac{a}{bc}+\dfrac{b}{ca}+\dfrac{c}{ab}\right)\ge2\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\)

\(\Leftrightarrow\dfrac{a}{bc}+\dfrac{b}{ca}+\dfrac{c}{ab}\ge\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\)

Vậy ta có đpcm.