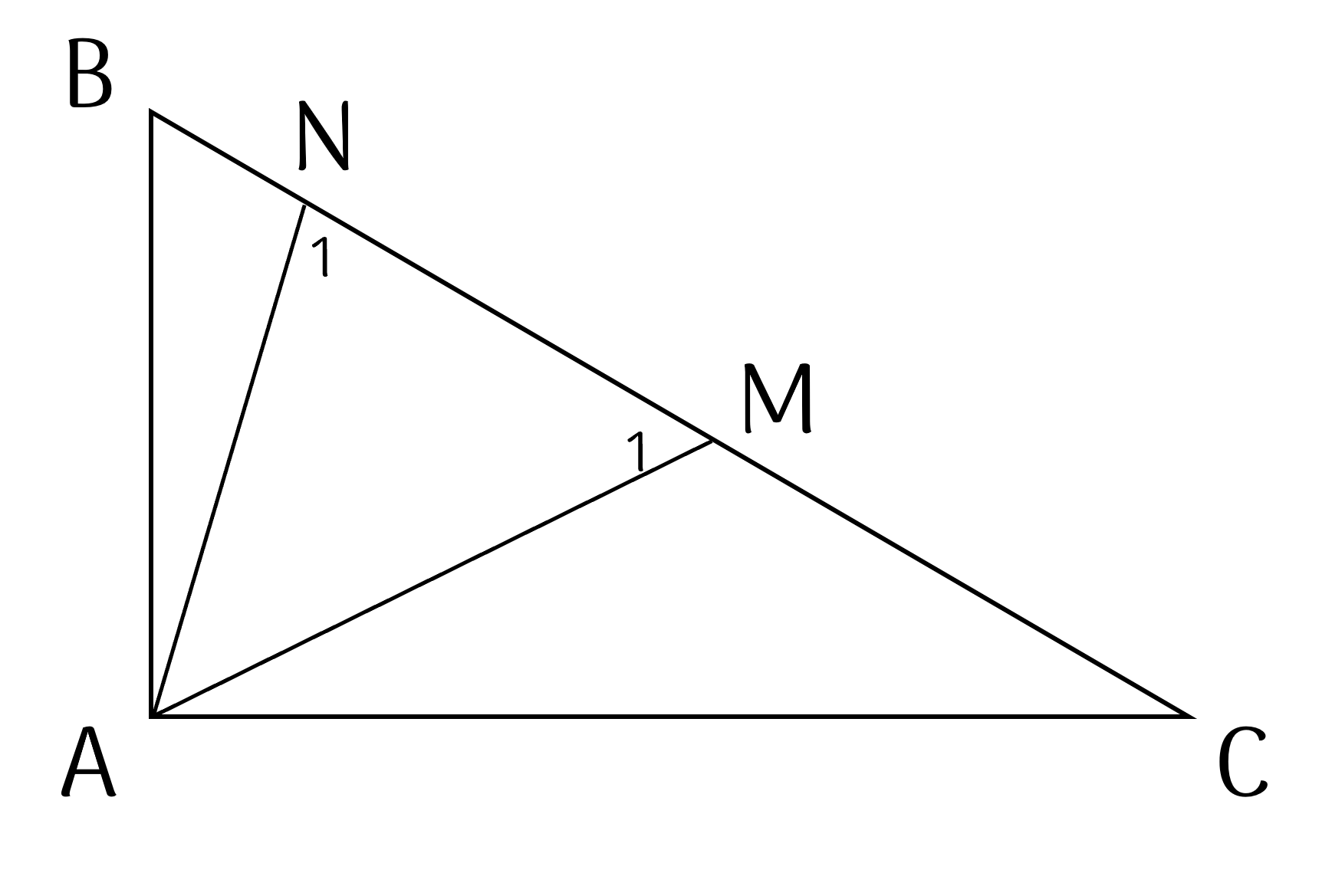
$BM = BA$ nên $\Delta BAM$ cân tại $B$.
Suy ra $\widehat{M_1} = \dfrac{180^{\circ} - \widehat{B}}2$.
$CN = CA$ nên $\Delta CAN$ cân tại $C$.
Suy ra $\widehat{N_1} = \dfrac{180^{\circ} - \widehat{C}}2$.
Suy ra $\widehat{N_1} + \widehat{M_1} = 180^{\circ} - \dfrac12(\widehat{B} + \widehat{C})$
nên $180^{\circ} - \widehat{N_1} - \widehat{M_1} = \dfrac12(\widehat{B} + \widehat{C})$
Trong $\Delta MAN$ có $\widehat{MAN} = 180^{\circ} - \widehat{N_1} - \widehat{M_1}$
nên $\widehat{MAN} = \dfrac12(\widehat{B} + \widehat{C}) = \dfrac12.90^{\circ} = 45^{\circ}$.












