Các câu hỏi tương tự
Cho tam giác ABC, AB>AC từ trung điểm M của BC vẽ 1 đường thẳng vuông góc với tia phân giác của góc A , cắt tia phân giác tại H , cắt AB ,AC lần lượt tại E và F chứng minh .
a, BE=CF
b, AE = (AB+AC):2
c, BE=(AB-AC) :2
d, góc BME = ( góc ACB - góc B) :2
cho tam giác ABC có AB > AC M là trung điểm của BC (MB = MC) từ M vẽ đường thẳng vuông góc với tia phân giác của góc A cắt tia phân giác tại H cắt AB,AC lần lượt tại E và F. CMR:
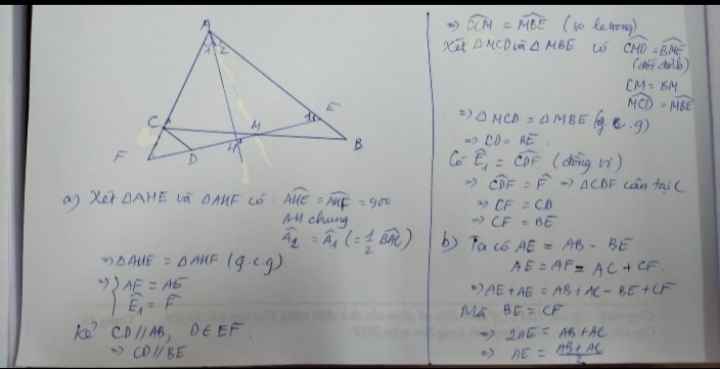
a) BE = CF
b) AE = AB+AC/2
BE = AB-AC/2
c) góc BME = GÓC ACB - B/2
Cho tam giác ABC có AB AC. Từ trung điểm M của Bc vẽ một đường thẳng vuông góc với tia phân giác của góc A, cắt tia phân giác tại H, cắt AB, AC lần lượt tại E và F. Chứng minh rằng: a) BE CFb) AB + AC AB - AC AE ______, BE ______ 2 2c) ACB - B Góc BME ______ 2Mọi người giúp mình với ạ, mình đang cần gấp.
Đọc tiếp
Cho tam giác ABC có AB > AC. Từ trung điểm M của Bc vẽ một đường thẳng vuông góc với tia phân giác của góc A, cắt tia phân giác tại H, cắt AB, AC lần lượt tại E và F. Chứng minh rằng:
a) BE = CF
b) AB + AC AB - AC
AE = ______, BE = ______
2 2
c) ACB - B
Góc BME= ______
2
Mọi người giúp mình với ạ, mình đang cần gấp.
cho tam giác ABC có AB > AC . Từ trung điểm M của BC vẽ một đường thẳng vuông góc với tia phân giác của góc A, cắt tia phân giác tại H, cắt AB, AC lần lượt tại E VÀ F. chứng minh rằng :
a) BE=CF
b) AE=\(\frac{AB+AC}{2}\); BE=\(\frac{AB-AC}{2}\)
c) \(\widehat{BME}=\frac{\widehat{ACB}-\widehat{B}}{2}\)
GIUP MIK NHA !!!!!!!!!!
Cho tam giác ABC có AB>AC. Từ trung điểm M của BC vẽ đường thẳng vuông góc với tia phân giác của góc A tại H, cắt AB, AC lần lượt tại E và F. Chứng minh:
a) EH = HF
b) 2 lần góc BME = góc ACB - góc B
c) EF2 chia 4 + AH2 = AE2
d) BE = CF
Cho tam giác ABC có AB>AC. M là trung điểm của BC, từ M vẽ MH vuông góc với tia phân giác của góc A tại H. Đường thẳng MH cắt AB và AC lần lượt tại E và F.
a) Chứng minh rằng: BE=CF.
b) Chứng minh rằng: AE=\(\frac{AB+AC}{2}\)
c) Chứng minh rằng góc BME=\(\frac{ACB-B}{2}\)
cho tam giác ABC có AB>AC . Điểm M là trung điểm của BC . Vẽ đường thẳng vuông góc với tia phân giác đó tại A ,cắt AB,AC làn lượt tại E,F .Chứng minh rằng :
a, BE=CF
b, AE=AB+AC/2
c, góc BAE .2 =góc ACB - góc B
giúp mình với nha thanks nhìu
Tam giác ABC có AB >AC. Từ trung điểm M của BC vẽ một đường thẳng vuông góc với tia phân của góc A, cắt tia phân giác tại H, cắt AB,AC lần lượt tại E và F. CMR:
a) BE=CF
b) AE=\(\frac{AB+AC}{2}\) ; BE=\(\frac{AB-AC}{2}\)
c) \(\widehat{BME}=\frac{\widehat{ACB}-\widehat{B}}{2}\)
Cho tam giác ABC ( AB > AC ) M là trung điểm của BC . Đường thẳng vuông góc với tia phân giác của góc A tại M cắt cạnh AB , AC lần lượt tại E và F và cắt tia phân giác của góc A tại H .
CMR :
a, EH = HF
b, 2 . góc BME = góc ACB - góc B
c, FE bình : 4 + AH bình = AE bình
d, BE = CF