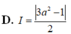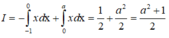Các câu hỏi tương tự
Cho a là số thực dương, tính tích phân
I
∫
-
1
a
|
x
|
d
x
theo a
Đọc tiếp
Cho a là số thực dương, tính tích phân I = ∫ - 1 a | x | d x theo a
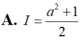
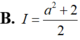
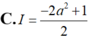
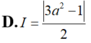
Cho số thực a0 Gỉa sử hàm số f(x) liên tục và luôn dương trên đoạn [0;a] thỏa mãn f(x).f(a-x) 1 Tính tích phân
I
∫
0
a
1
1
+
f
(
x
)
d
x
A. a/3 B. a/2 C. a D. 2a/3
Đọc tiếp
Cho số thực a>0 Gỉa sử hàm số f(x) liên tục và luôn dương trên đoạn [0;a] thỏa mãn f(x).f(a-x) = 1 Tính tích phân I = ∫ 0 a 1 1 + f ( x ) d x
A. a/3
B. a/2
C. a
D. 2a/3
Cho a,b là các số thực dương thỏa mãn
∫
a
b
f
(
x
)
d
x
1
. Tích phân
I
∫
ln
x
ln
b
e
x
.
f
e
x
c...
Đọc tiếp
Cho a,b là các số thực dương thỏa mãn ∫ a b f ( x ) d x = 1 . Tích phân I = ∫ ln x ln b e x . f e x có giá trị bằng bao nhiêu?
A. I = 0.
B. I = 1.
C. I = |a-b|.
D. I = e.
Cho số thực a0. Giả sử hàm số f(x) liên tục và luôn dương trên đoạn [0;a] thỏa mãn f(x).(fa-x) 1 Tính tích phân
∫
0
1
1
1
+
f
(
x
)
d
x
A. I a/2 B. I a C. I 2a/3 D. I a/3
Đọc tiếp
Cho số thực a>0. Giả sử hàm số f(x) liên tục và luôn dương trên đoạn [0;a] thỏa mãn f(x).(fa-x) = 1 Tính tích phân ∫ 0 1 1 1 + f ( x ) d x
A. I = a/2
B. I = a
C. I = 2a/3
D. I = a/3
Cho a là một số thực dương. Tính
I
∫
0
a
e
x
(
x
+
1
)
d
x
Đọc tiếp
Cho a là một số thực dương. Tính I = ∫ 0 a e x ( x + 1 ) d x
![]()
![]()
![]()
![]()
Cho tích phân
I
∫
1
2
ln
x
x
2
d
x
b
c
+
a
ln
2
với a là số thực, b và c là các số nguyên dương, đồng thời
b
c
là phân số tối giản. Tính giá trị của biểu thức...
Đọc tiếp
Cho tích phân I = ∫ 1 2 ln x x 2 d x = b c + a ln 2 với a là số thực, b và c là các số nguyên dương, đồng thời b c là phân số tối giản. Tính giá trị của biểu thức
P = 2a + 3b + c.
A. P=6
B. P=-6
C. P=5
D. P=4
Cho hàm số yf(x) liên tục trên R và thỏa mãn f(x) + f(
π
3
-
x
)
1
2
sin
x
cos
x
(
8
cos
3
x
+
1
)
,
∀
x
∈...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và thỏa mãn f(x) + f( π 3 - x )= 1 2 sin x cos x ( 8 cos 3 x + 1 ) , ∀ x ∈ R Biết tích phân I= ∫ 0 π 3 f ( x ) d x được biểu diễn dưới dạng I= a b ln c d ; a , b , c , d ∈ Z và các phân số a b ; c d là các phân số tối giản. Tính S= a 3 + a b - c + d
![]()
![]()
![]()
![]()
Tính tích phân
I
∫
0
2
3
x
+
x
-
4
d
x
ta được kết quả
I
a
+
b
ln
c
( với a, b, c là các số nguyên dương). Khi đó giá trị của biểu thức
T...
Đọc tiếp
Tính tích phân I = ∫ 0 2 3 x + x - 4 d x ta được kết quả I = a + b ln c ( với a, b, c là các số nguyên dương). Khi đó giá trị của biểu thức T = a 3 + 3 b 2 + 2 c bằng:
A. 55
B. 36
C. 38
D. 73
Biết f(x) là hàm số liên tục trên
ℝ
, a là số thực thỏa mãn
0
a
π
và
∫
0
a
f
(
x
)
d
x
∫
0
π
f
(
x
)
d
x
1
. Tính tích phân
∫
0
π
f...
Đọc tiếp
Biết f(x) là hàm số liên tục trên ℝ , a là số thực thỏa mãn 0 < a < π và ∫ 0 a f ( x ) d x = ∫ 0 π f ( x ) d x = 1 . Tính tích phân ∫ 0 π f x d x bằng:
A. 0
B. 2
C. 1 2
D. 1