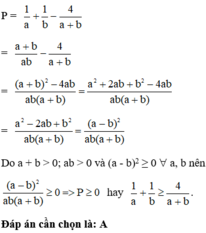Các câu hỏi tương tự
Cho biết a < b. Trong các khẳng định sau, số khẳng định đúng là?
(I) a - 1 < b - 1 (II) a - 1 < b (III) a + 2 < b + 1
A. 1
B. 2
C. 3
D. 0
Cho a,b,c,d >0. Chứng minh:
\(\frac{1}{a^4+b^4+c^4+abcd^{ }}+\frac{1}{a^4+b^4+d^4+abcd}+\frac{1}{a^4+c^4+d^4+abcd^{ }^{ }}+\frac{1}{b^4+c^4+d^4+abcd}\le\frac{1}{abcd}\)
Cho 4 số a,b,c,d khác 0 thỏa mãn abcd=1 và a+b+c+d= 1/a +1/b +1/c +1/d . CMR tồn tại 2 số trong 4 số đó bằng 1.
a-b+c=0; c=5d. Tính A:
A= (1-\(\dfrac{a}{b}\))(1-\(\dfrac{b}{c}\))(1-\(\dfrac{c}{a}\))(\(\dfrac{a-b}{d}\)-4)
Bài5: cho a,b,c0.CMR1, 2/a+1/b 4/a+b2, 1/a+1/b+1/c a/a+b+cBài 6: cho a,b0 cmr1, a^3+b^4ab(a+b)2, a^4+b^4ab(a^2+b^2)3, a5+b5ab(a^3+b^3)Bài 7 cho a,b,c0 cmr1/a^3+b^3+abc +1/b^3+c^3+abc+1/c^3+a^3+2 1/abcBài 8cho a,b,c0;abc11, 1/a^3+b^3+2 +1/b^3+c^3+2 +1/c^3+a^3+2 12,ab/a^5+b^5+ab +bc/b^5+c^5+bc + ca/c^5+a^5+ca 1
Đọc tiếp
Bài5: cho a,b,c>0.CMR
1, 2/a+1/b >= 4/a+b
2, 1/a+1/b+1/c>= a/a+b+c
Bài 6: cho a,b>=0 cmr
1, a^3+b^4>=ab(a+b)
2, a^4+b^4>=ab(a^2+b^2)
3, a5+b5>=ab(a^3+b^3)
Bài 7 cho a,b,c>0 cmr
1/a^3+b^3+abc +1/b^3+c^3+abc+1/c^3+a^3+2 <1/abc
Bài 8cho a,b,c>0;abc=1
1, 1/a^3+b^3+2 +1/b^3+c^3+2 +1/c^3+a^3+2 =< 1
2,ab/a^5+b^5+ab +bc/b^5+c^5+bc + ca/c^5+a^5+ca =<1
a) cho a>0,b>0,c>0
C/m (a+b+c)(1/a+1/b+1/c) >=1/9
b) cho a,b,c thỏa mãn: a+b+c=0 và a2+b2+c2=2011.Tính A=a4+b4+c4
mọi người giúp vs nha
Chứng minh :
a) (x+4)(x+7)(x+8)(x+11)+36>=0 . Dấu "=" xảy ra khi nào ?
b) Cho a,b,c>0, a+b+c =1 :
Chứng minh
* 1/a+b +1/a+c +1/b+c>4
* a+2b+c>= 4(1-a)(1-b)(1-c)
Cho a, b, c, d > 0 và a + b + c + d = 4. Tìm Min M = 1/(a^2 + 1) + 1/(b^2 + 1) + 1/(c^2 + 1) + 1/(d^2 + 1)
Cho a, b, c, d > 0 và a + b + c + d = 4. Tìm Min M = 1/(a^2 + 1) + 1/(b^2 + 1) + 1/(c^2 + 1) + 1/(d^2 + 1)
Cho 4 số a,b,c,d khác 0 thỏa mãn abcd=1 và a+b+c+d=1/a+1/b+1/c+/1d. chứng minh rằng tồn tại tích hai số trong 4 số bằng 1