Từ 3 hình vuông còn lại ta chia mỗi hình vuông thành 4 hình vuông nhỏ thì sẽ có 12 hình vuông. Từ 12 hình vuông đó ta được 4 phần bằng nhau. Mỗi phần gồm 3 hình nhỏ 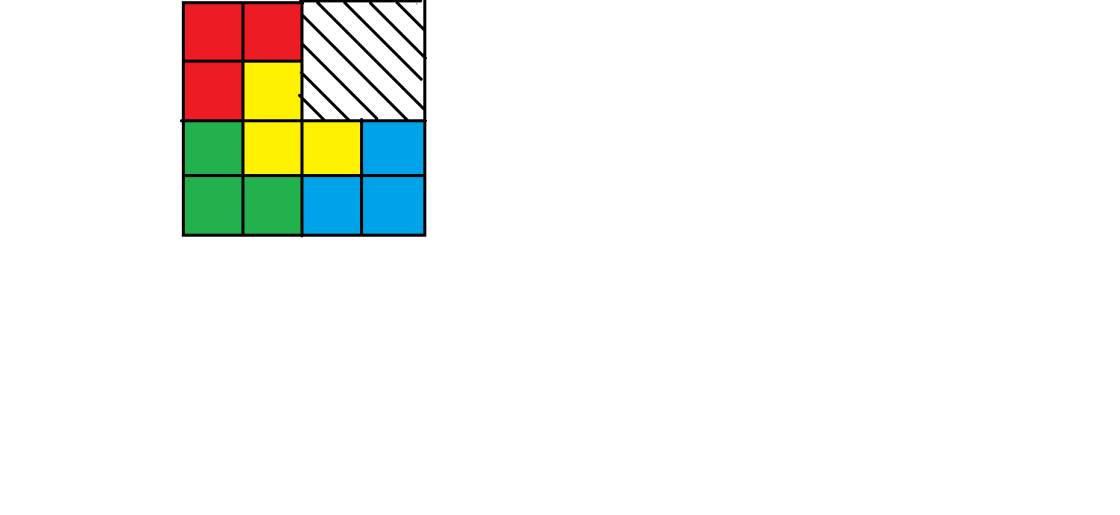
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho hình bình hành ABCD có tâm (giao hai đường chéo) là O.a) Chứng minh rằng mỗi đường thẳng d đi qua O đều chia hình bình hành thành haiphần có chu vi bằng nhau và diện tích bằng nhau.b) Một đường thẳng d chia hình bình hành thành hai phần có diện tích bằng nhau,chứng minh rằng nó đi qua O.c) Một đường thẳng d chia hình bình hành thành hai phần có chu vi bằng nhau, chứngminh rằng nó đi qua O.
Đọc tiếp
Cho hình bình hành ABCD có tâm (giao hai đường chéo) là O.
a) Chứng minh rằng mỗi đường thẳng d đi qua O đều chia hình bình hành thành hai
phần có chu vi bằng nhau và diện tích bằng nhau.
b) Một đường thẳng d chia hình bình hành thành hai phần có diện tích bằng nhau,
chứng minh rằng nó đi qua O.
c) Một đường thẳng d chia hình bình hành thành hai phần có chu vi bằng nhau, chứng
minh rằng nó đi qua O.
Đố. Tính diện tích phần hình còn lại mà không cần đo.
Từ một miếng tôn hình vuông có cạnh bằng a + b, bác thợ cắt đi một miếng cũng hình vuông có cạnh bằng a – b (cho a > b). Diện tích phần hình còn lại là bao nhiêu? Diện tích phần hình còn lại có phụ thuộc vào vị trí cắt không?
Cho tam giác ABC vuông tại A, đường cao AH chia cạnh BC thành hai đoạn thẳng HB = 7cm và HC = 18cm. Điểm E thuộc đoạn thẳng HC sao cho đường thẳng đi qua E và vuông góc với BC chia tam giác ABC thành hai phần có diện tích bằng nhau. Tính CE.
A. 15cm
B. 12cm
C. 10cm
D. 8cm
Cho một hình ngũ giác có ba đường thẳng d1,d2,d3 cắt nhau tại 3 điểm A,B,C thuộc miền trong ngũ giác sao cho 1 đường thẳng chia ngũ giác thành 2 phần co diện tích bằng nhau. Chứng minh rằng: S của ABC<1/4 S của ngũ giác đã cho
Cho một hình ngũ giác có ba đường thẳng d1,d2,d3 cắt nhau tại 3 điểm A,B,C thuộc miền trong ngũ giác sao cho 1 đường thẳng chia ngũ giác thành 2 phần co diện tích bằng nhau. Chứng minh rằng: S của ABC<1/4 S của ngũ giác đã cho
Cho tam giác ABC vuông tại A. Đương cao và đường trung tuyến thuộc đỉnh A chia góc vuông ra thành ba phần bằng nhau. Biết rằng diện tích tam giác AHB=R . Tính diện tích hình tam giác ABC
cho hình vuông ABCD . Qua giao điểm O của các đường chéo AC , BD kẻ đường thẳng vuông góc với nhau MON ,POQ cắt AD , BC , DC , AB theo thứ tự tại M , N , P , Q
a) các tam giác OAM , ODP , OCN , OBQ có diện tích bằng nhau
b) hai đường thẳng MN , PQ chia hình vuông thành bốn phần có diện tích bằng nhau
Cho hình thang ABCD có đáy nhỏ CD và đáy lớn AB. Hãy chia hình thang đã cho thành hai phần có diện tích bằng nhau bằng một đường thẳng đi qua đỉnh D của nó.
Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 3,5cm và HC = 9cm. Điểm E thuộc đoạn thẳng HC sao cho đường thẳng đi qua E và vuông góc với BC chia tam giác ABC thành hai phần có diện tích bằng nhau. Tính CE.
A. 10cm
B. 6cm
C. 5cm
D. 7,5cm









