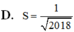Phương pháp:
Sử dụng tính chất của tích phân:
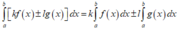
Cách giải:
![]()
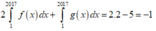
Chọn: B
Phương pháp:
Sử dụng tính chất của tích phân:
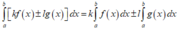
Cách giải:
![]()
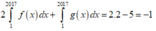
Chọn: B
Hàm số y=f(x) có đồ thị y=f '(x) như hình vẽ
.
Xét hàm số g ( x ) = f ( x ) - 1 3 x 3 - 3 4 x 2 + 3 2 x + 2017
Trong các mệnh đề dưới đây
(I) .g(0)<g(1)
(II) . m i n x ∈ [ - 3 ; 1 ] g ( x ) = g ( - 1 )
(III) Hàm số g(x)nghịch biến trên (-3;-1).
(IV). m a x x ∈ [ - 3 ; 1 ] g ( x ) = m a x { g ( - 3 ) , g ( 1 ) }
Số mệnh đề đúng là
A.2.
B.1.
C.3
D.4.
Cho hàm số f(x) xác định trên R\{1} thỏa mãn f ' ( x ) = 1 x - 1 , f ( 0 ) = 2017 ; f ( 2 ) = 2018 . Tính S = f(3)-f(-1)
A. S = 1
B. S = ln2
C. S = ln4035
D. S = 4
Cho hàm số f(x) liên tục trên ℝ và f(x) ≠ 0 với mọi x ∈ ℝ . f ' ( x ) = ( 2 x + 1 ) f 2 ( x ) và f(1)=-0,5. Biết rằng tổng f(1)+f(2)+f(3)+...+f(2017)= a b với a b tối giản.
Mệnh đề nào dưới đây đúng?
![]()
![]()
![]()
![]()
Cho hàm số f ( x ) = e 1 + 1 x 2 + 1 ( x + 1 ) 2 , biết rằng f ( 1 ) . f ( 2 ) . f ( 3 ) . . . f ( 2017 ) = e m n với m, n là các số tự nhiên và m 2 tối giản. Tính m - n 2
A. m - n 2 = 2018
B. m - n 2 = 1
C. m - n 2 = -2018
D. m - n 2 = -1
Cho hàm số y= f( x) ) liên tục trên R. Hàm số y= f’ (x) có đồ thị như hình vẽ. Hàm số y = g ( x ) = f ( x ) + 2017 - 2018 x 2017 có bao nhiêu cực trị?
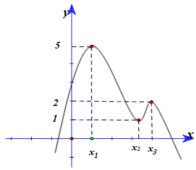
A. 1.
B. 2.
C. 3.
D. 4.
Cho hàm số y = f(x) có đạo hàm liên tục trên ℝ . Đồ thị hàm số y = f'(x) được cho như hình vẽ bên.
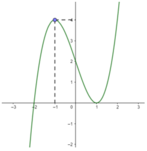
Số điểm cực trị của hàm số g(x) = f(x-2017) - 2018x + 2019 là:
A. 1.
B. 3.
C. 2.
D. 0.
Cho hàm số y = f(x) có đạo hàm trên R. Đồ thị hàm số y= f’(x) như hình vẽ bên dưới
Số điểm cực trị của hàm số y= g( x)= f( x- 2017) – 2018x+ 2019 là
A. 1
B. 2
C.3
D. 4
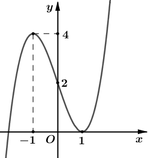
Gọi F(x) là một nguyên hàm của hàm số f(x)= 5 x thỏa mãn f(0)= 1 ln 5 . Tính giá trị biểu thức T=F(0)+F(1)+F(2)+...+F(2017)
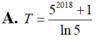
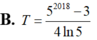
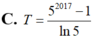
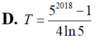
Cho hàm số f ( x ) = a x 4 + b x 2 + c v ớ i a > 0 , c > 2017 , a + b + c < 2017 . Số cực trị của hàm số y = | f ( x ) - 2017 | là
A. 1
B. 5
C. 3
D. 7
Cho biểu thức f ( x ) = 1 2018 x + 2018 . Tính tổng
S = 2018 [ f ( - 2017 ) + f ( - 2016 ) + . . . + f ( 0 ) + f ( 1 ) + . . . + f ( 2018 ) ]
![]()
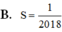
![]()