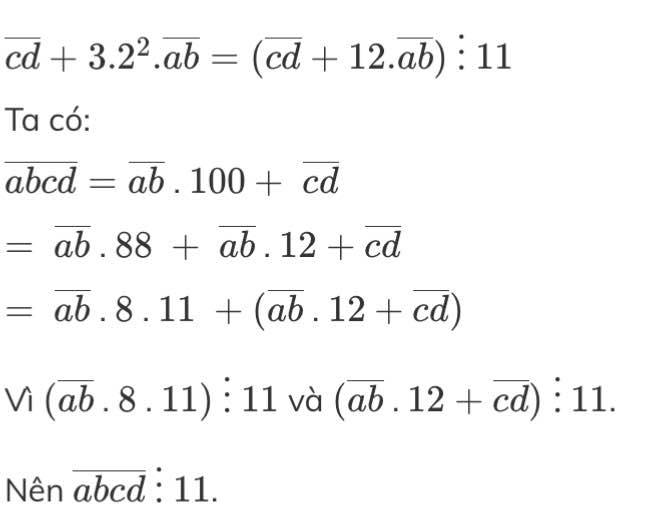Ta có:
.
. .
. . .
Vì . . và . .
Nên .
abcd=1111; 2222; 3333; 4444;...
Ta có:
.
. .
. . .
Vì . . và . .
Nên .
Ta có:
.
. .
. . .
Vì . . và . .
Nên .
Ta có:
.
. .
. . .
Vì . . và . .
Nên .
Theo giả thiết:
Ta có:
.
. .
. . .
Vì . . và . .
Nên .
Theo giả thiết:
Ta có:
.
. .
. . .
Vì . . và . .
Nên .
Theo giả thiết:
Ta có:
.
. .
. . .
Vì . . và . .
Nên .
Ta có:
.
. .
. . .
Vì . . và . .
Nên .
Theo bài ta có :
abcd = ab . 100 + cd
= ab . 88 + ab . 12 + cd
= ab . 8 . 11 + ( ab . 12 + cd )
Vì ( ab . 8 . 11 ) ⋮ 11 và ( ab . 12 + cd ) ⋮ 11 .
Nên abcd ⋮ 11.
Ta có :
abcd = ab . 100 + cd
= ab . 88 + ab . 12 .cd
= ab . 8 .11 + ( ab . 12 + cd )
Vì ab . 8 . 11 ⋮ 11 và ( ab .12 + cd ) ⋮ 11
Nên abcd ⋮
abcd chia hết 11
Ta có:
.
. .
. . .
Vì . . và . .
Nên
Ta có:
.
. .
. . .
Vì . . và . .
Nên .
cd+ 3.22.ab= ( cd+12.ab)
ta có :
abcd = ab.100+ cd
=ab.88+ab.12+cd
=ab.8.11+(ab.12+cd)
vì (ab.8.11) .và (ab.12+cd) ..
Nên abcd .
Theo giả thiết:
\overline{cd} + 3.2^2.\overline{ab} = (\overline{cd} + 12.\overline{ab})
Theo giả thiết:
\overline{cd} + 3.2^2.\overline{ab} = (\overline{cd} + 12.\overline{ab})
Theo giả thiết:
Ta có:
.
. .
. . .
Vì . . và . .
Nên .
Theo giả thiết:
Ta có:
.
. .
. . .
Vì . . và . .
Nên .
abcd chia hết cho 11
abcd:11 .Vì abcd=a+b+c+d:11
Ta có:
.
. .
. . .
Vì . . và . .
Nên .
.
. .
. . .
Vì . . và . .
Nên .
Cho bốn chữ a;b;c;d với a và c khác 0 thoả mãn (cd+3.4.ab) chia hết cho 11 Chứng minh abcd chia hết cho 11