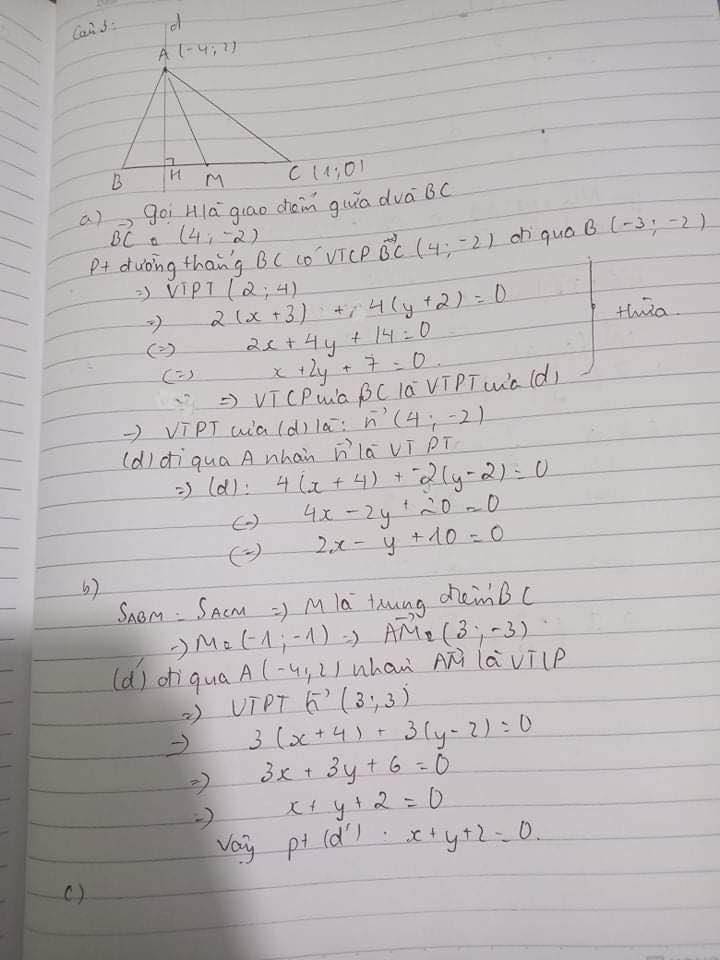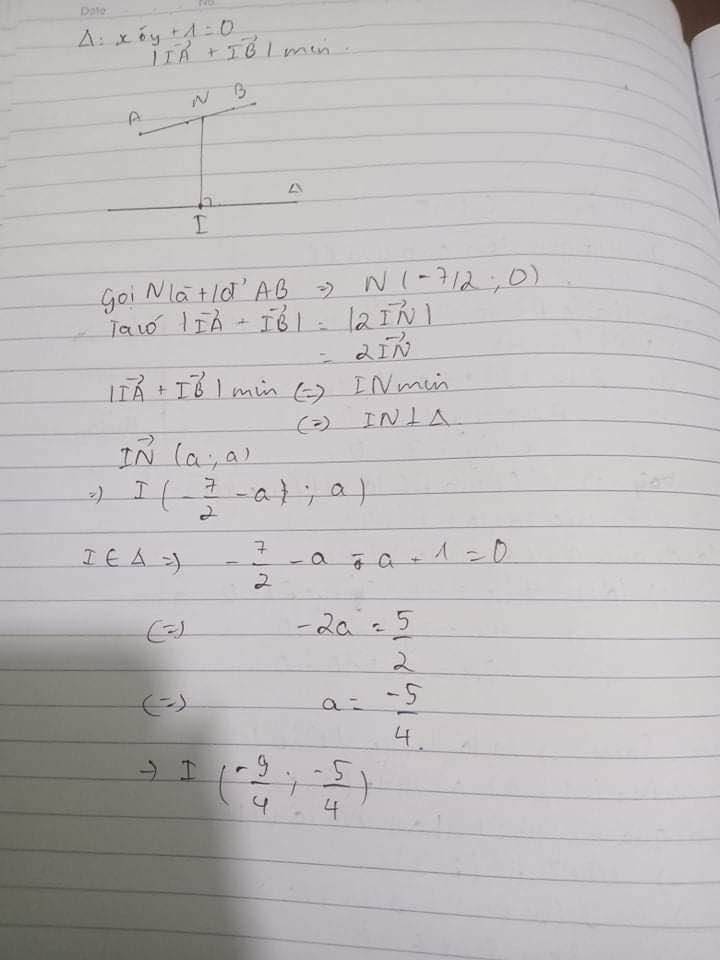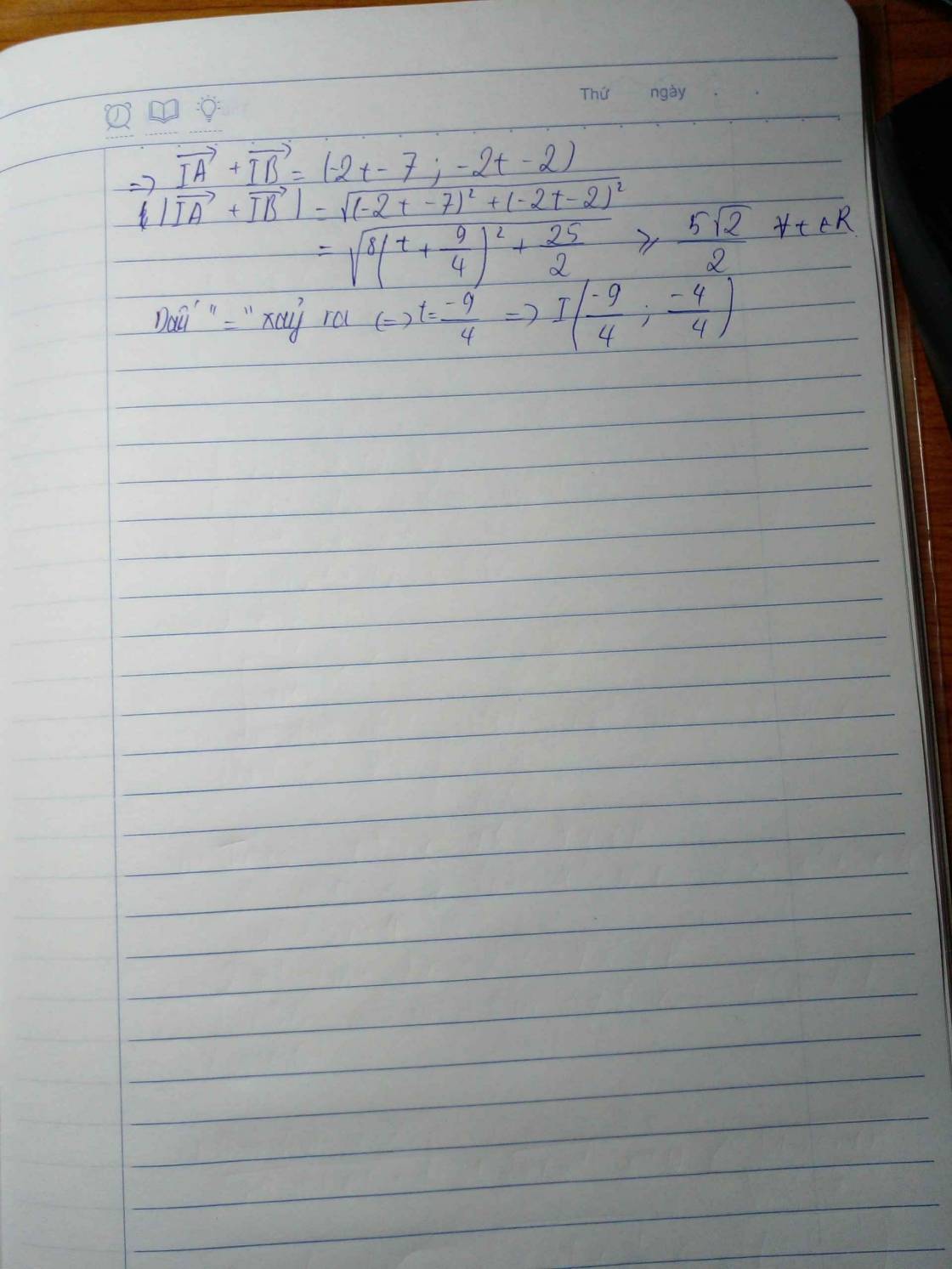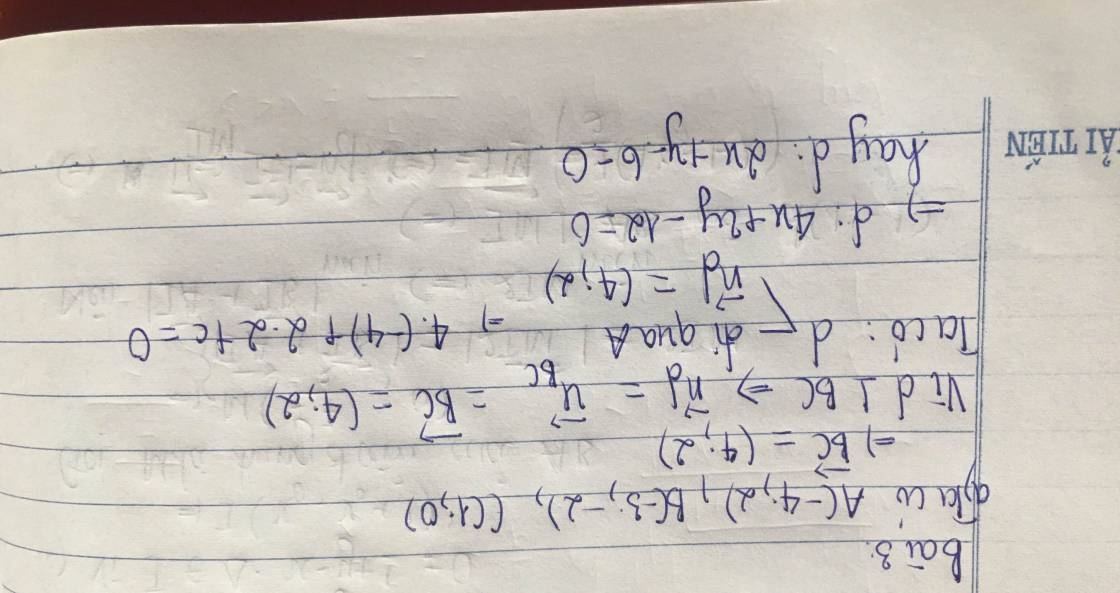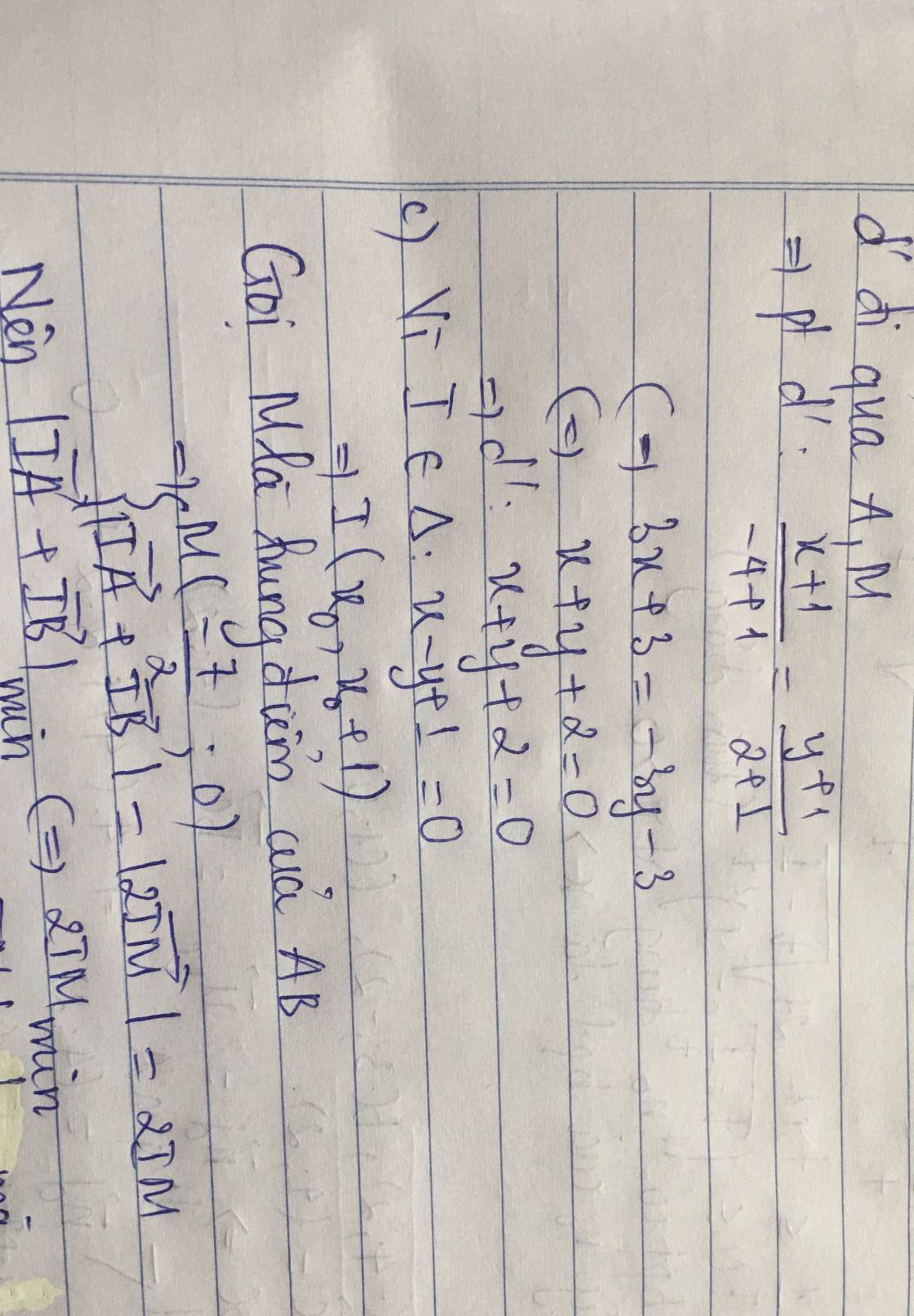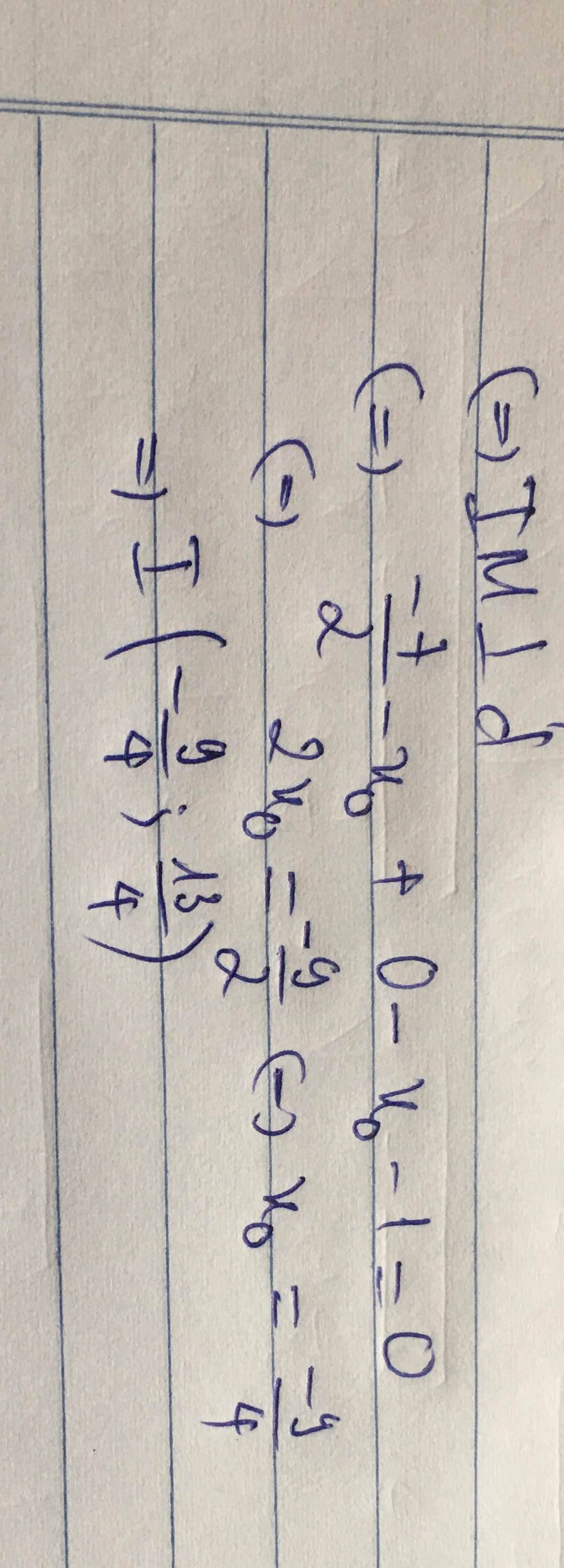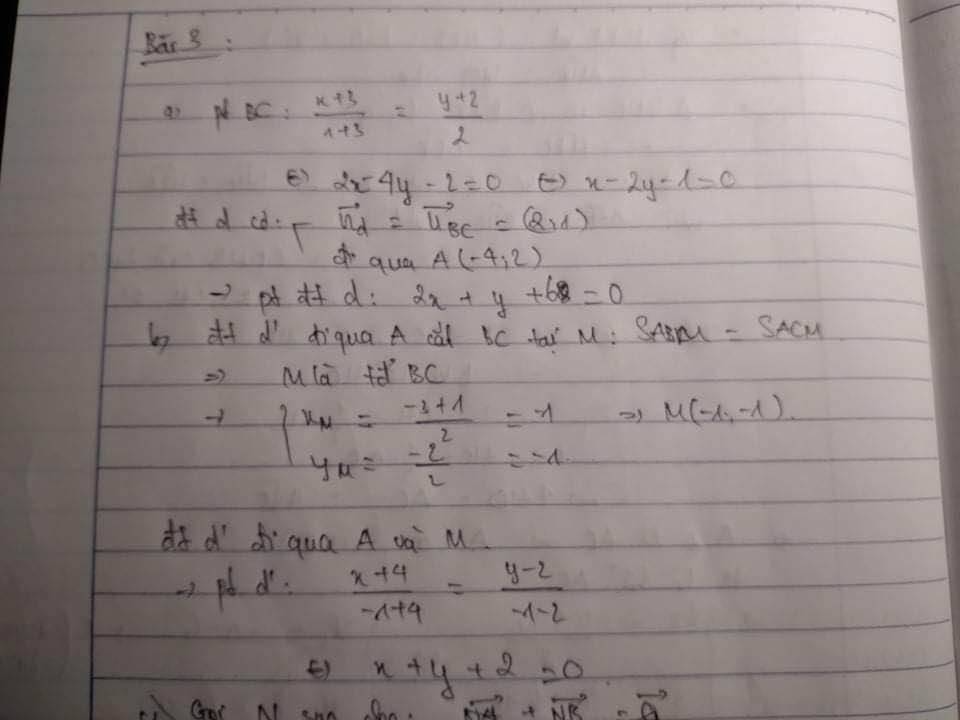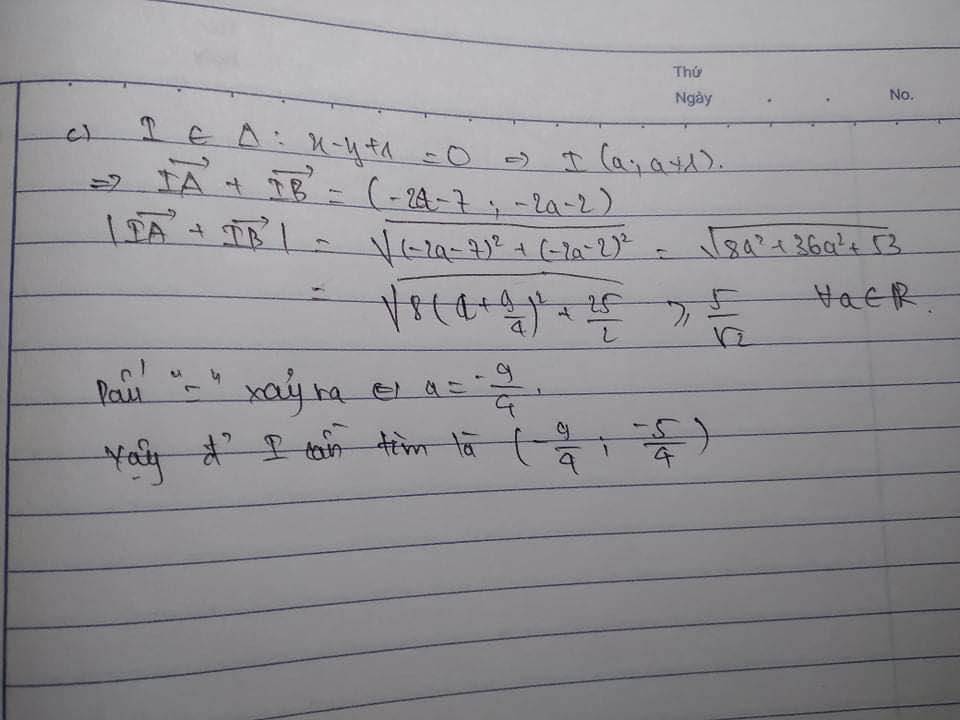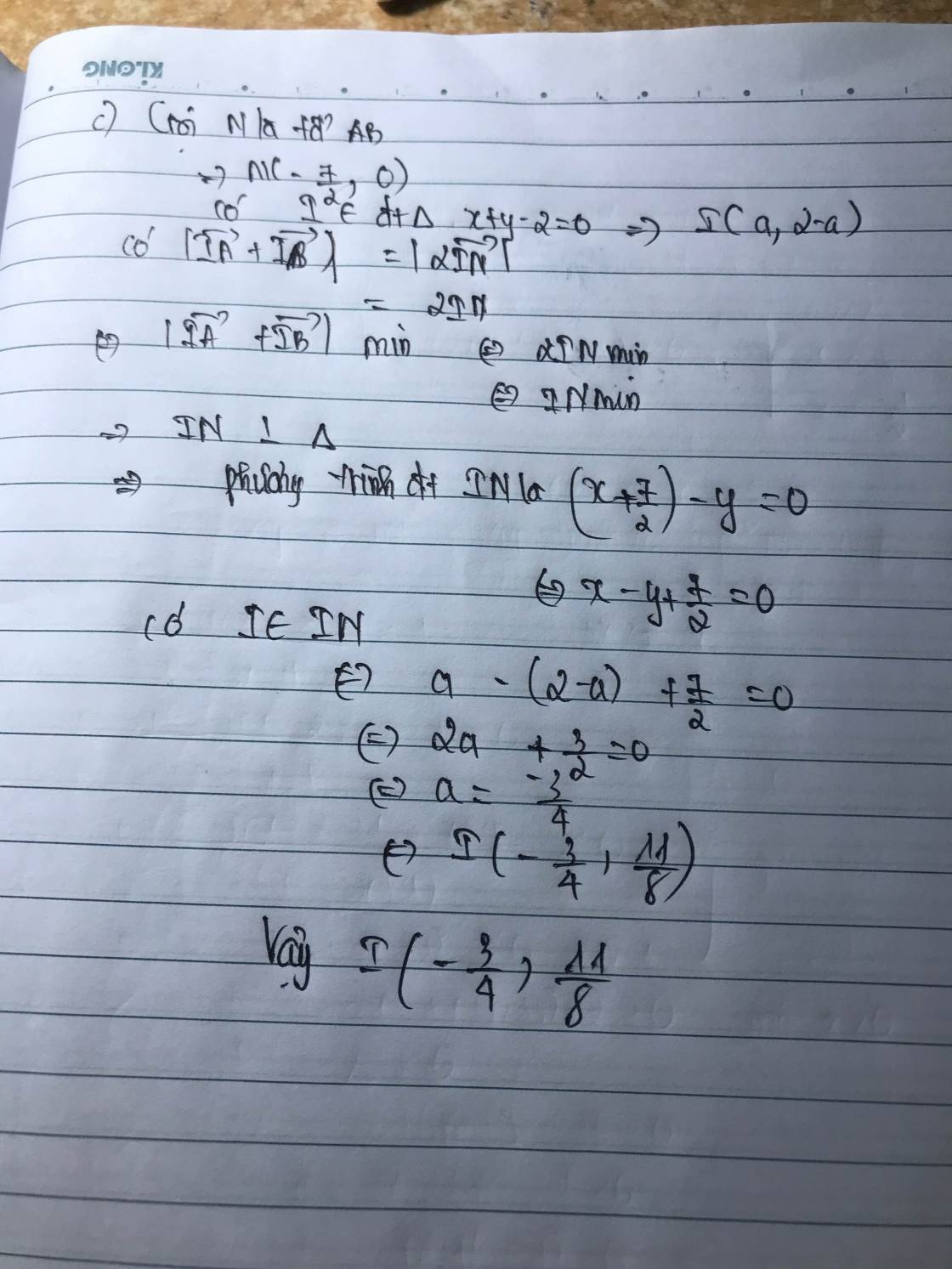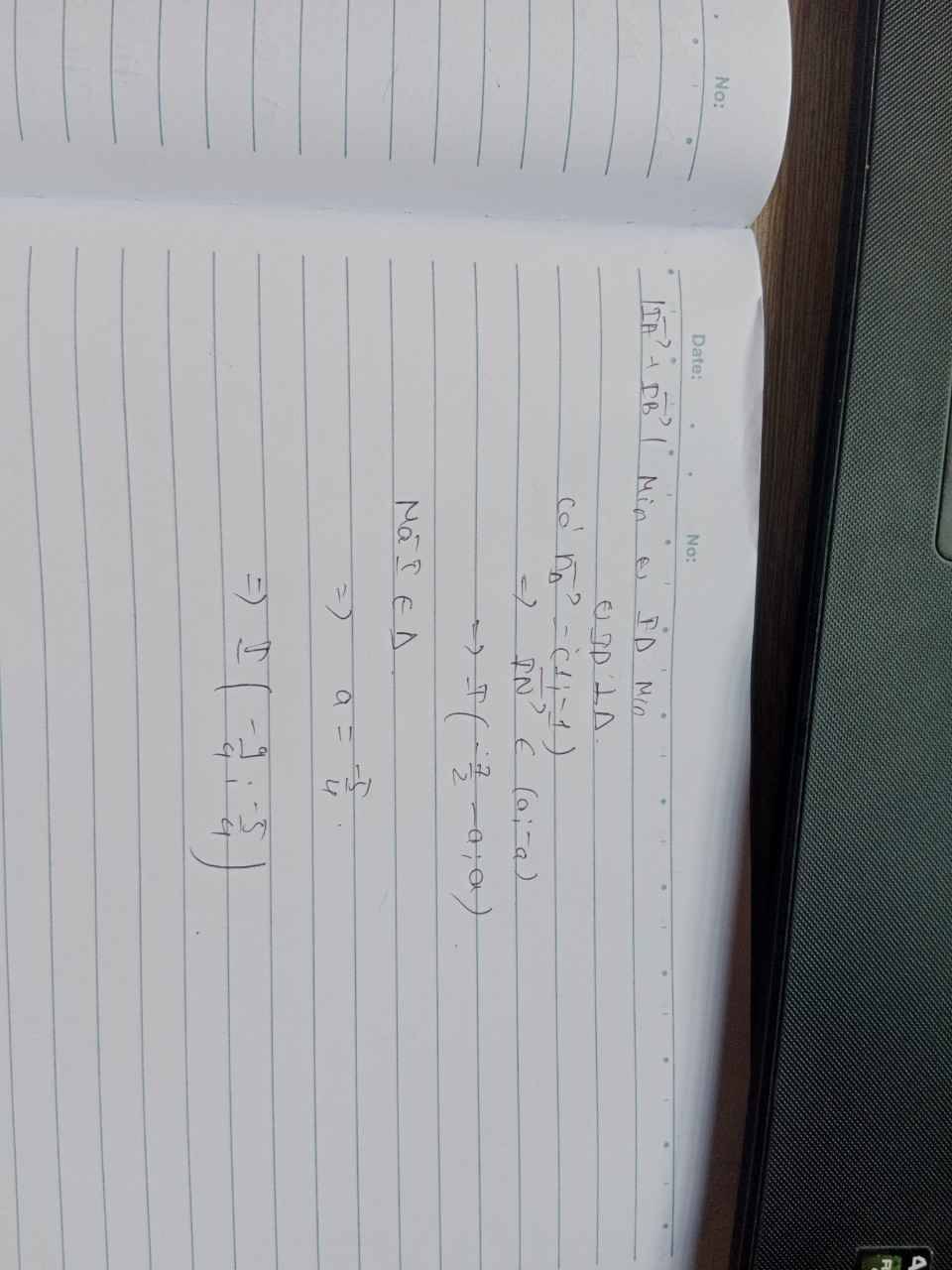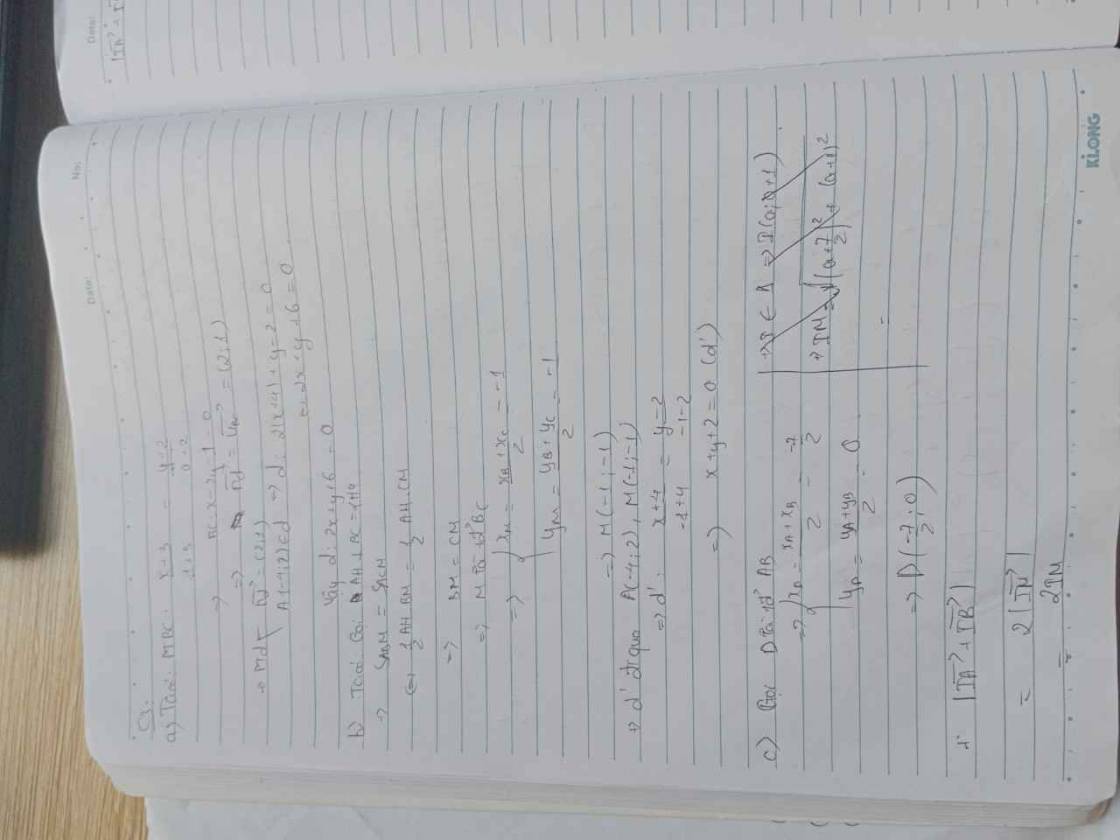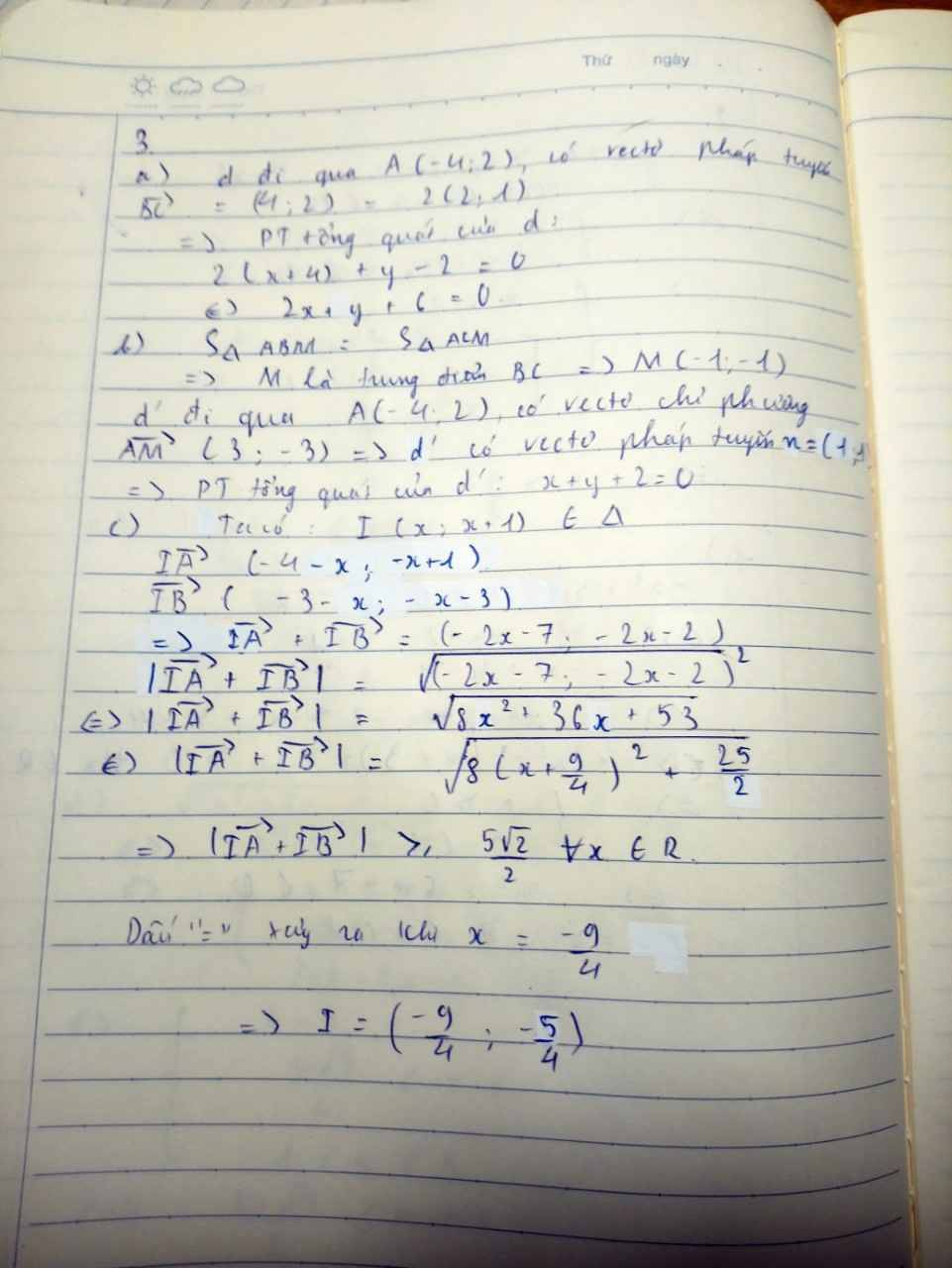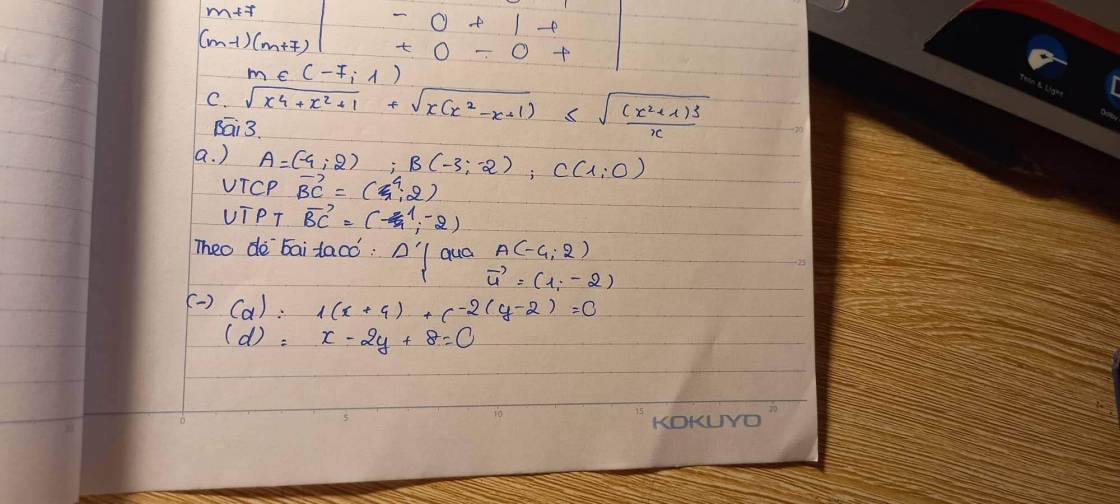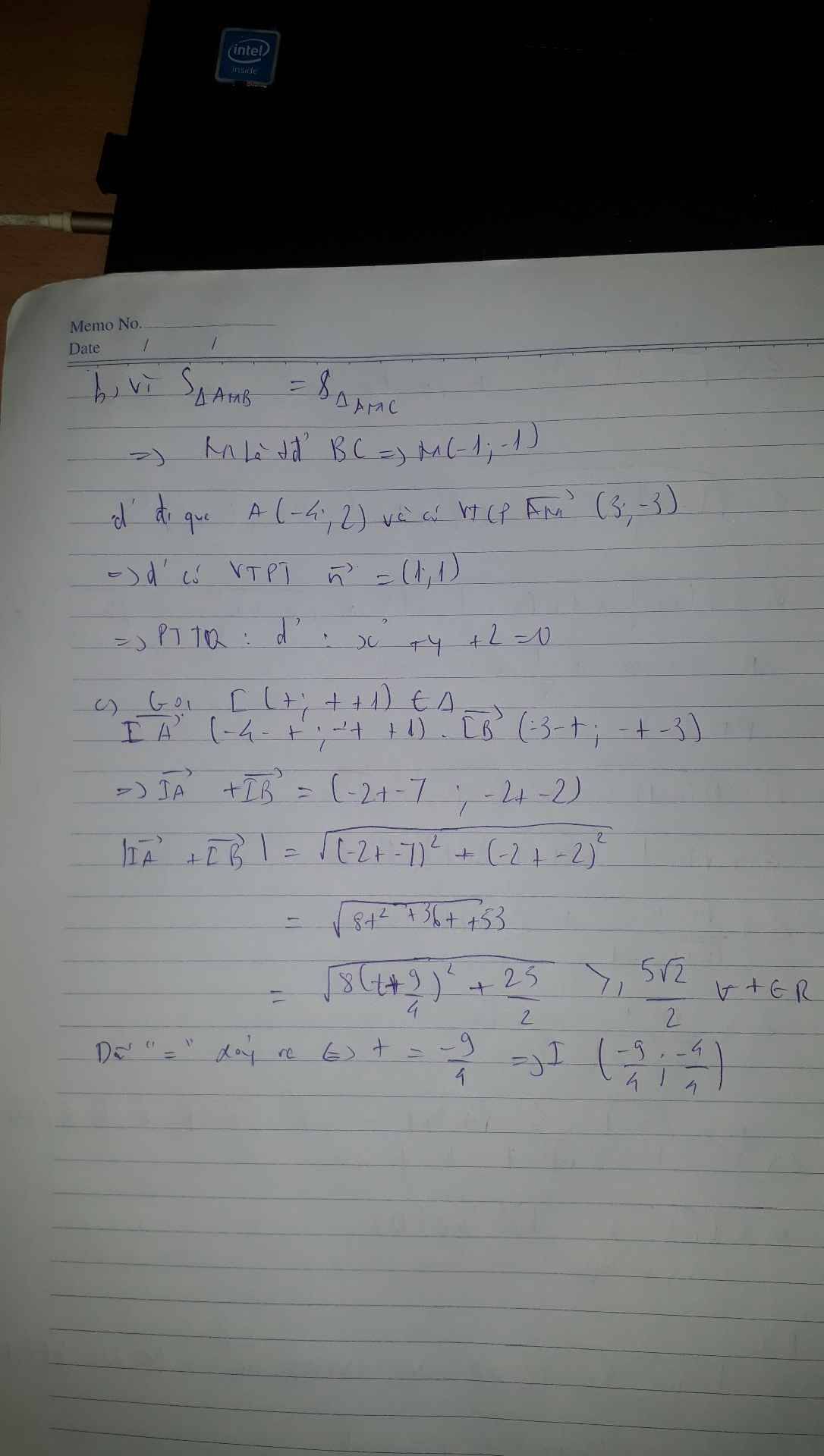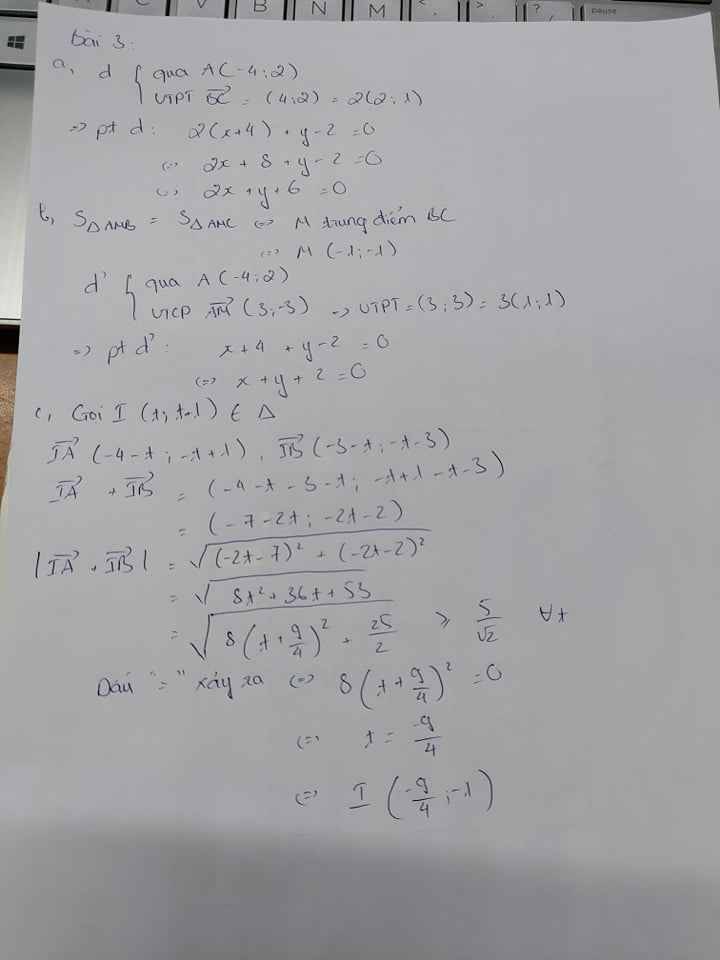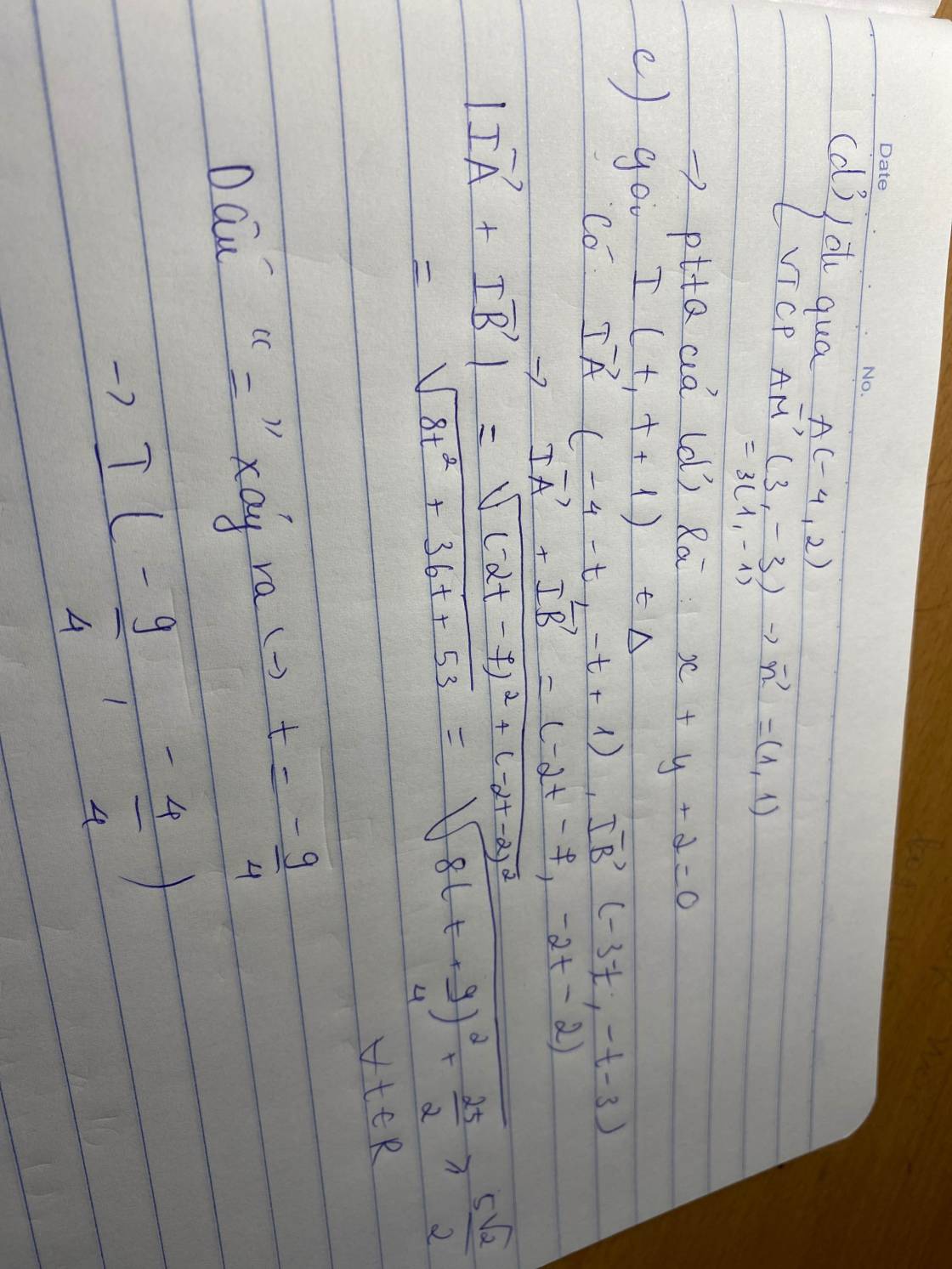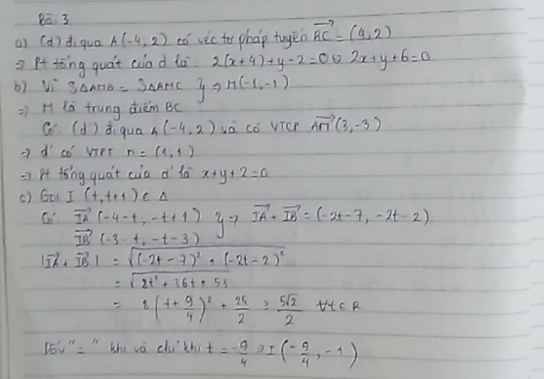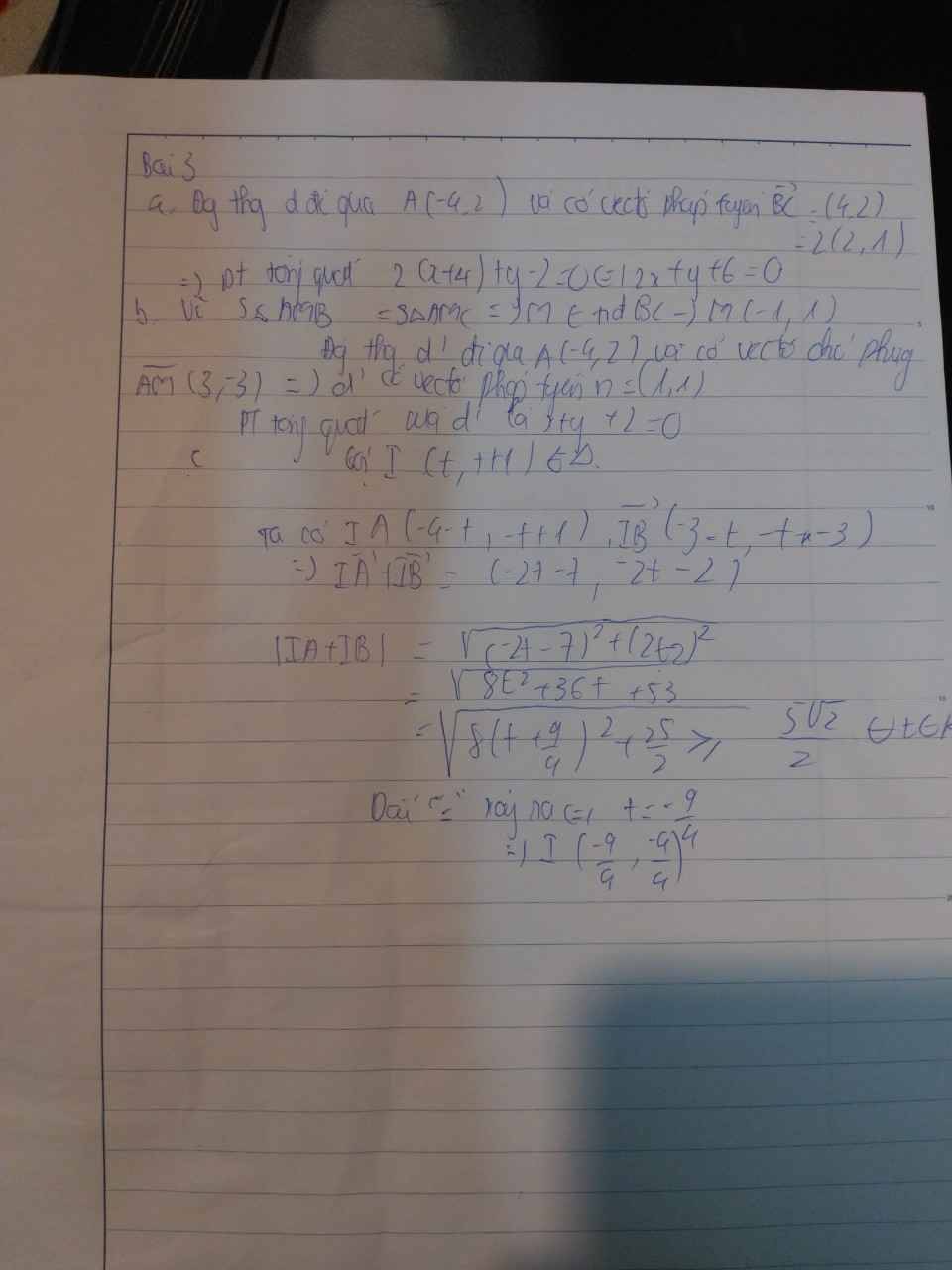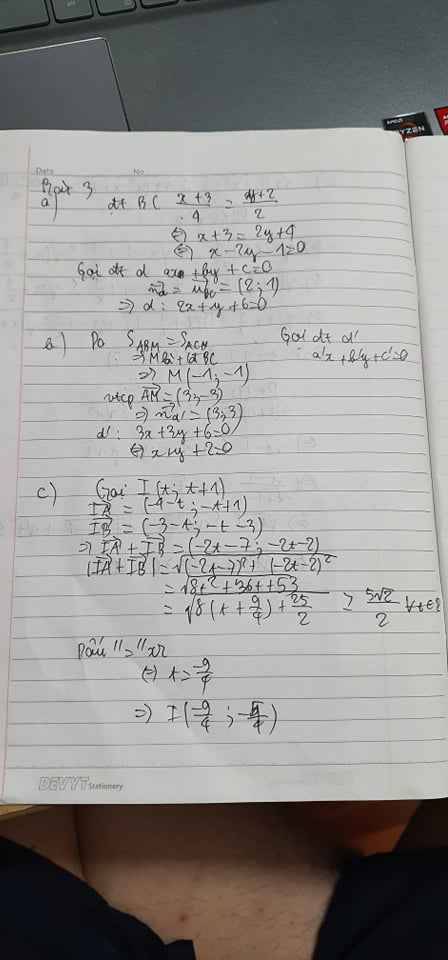Question

Câu 3 (3 điểm). Trong mặt phẳng $O x y$ cho tam giác $ABC$ với điểm $A(-4 ; 2), B(-3 ;-2), C(1 ; 0)$.

a) Viết phương trình tổng quát của đường thẳng $d$ đi qua điểm $A$ và vuông góc với đường thẳng $BC$.

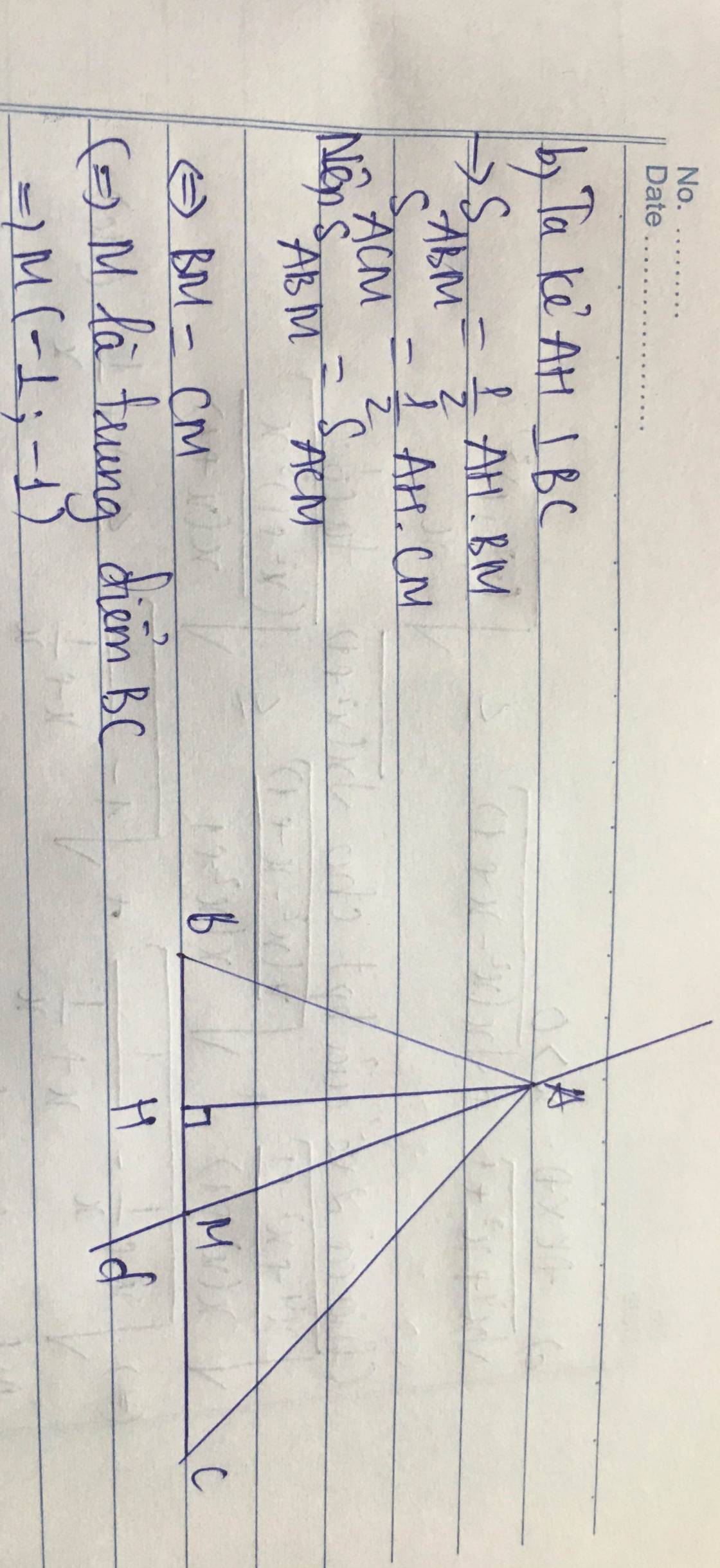
b) Viết phương trình tổng quát đường thẳng $d'$ đi $A$ cắt cạnh $BC$ tại $M$ sao cho diện tích tam giác $ABM$ bằng diện tích tam giác $ACM$.

c) Tìm điểm $I$ thuộc đường thẳng $\Delta: x-y+1=0$ sao cho $|\overrightarrow{IA}+\overrightarrow{IB}|$ đạt giá trị nhỏ nhất.

Answer 1

  

Answer 2

Answer 3

Answer 4

Answer 5

    

Answer 6

a) Đường thẳng d' đi qua A(4,2) va có vecto pháp tuyến \(\overrightarrow{BC}\) =(4,2)=2(2,1)

Ta có phương trình tổng quát của d là:2(x+4)+y-2=0\(\Leftrightarrow\) 2x+y+6=0

b) Vì \(S\Delta AMB=S\Delta AMC\) suy ra M là trung điểm của BC \(\Rightarrow\)M(-1,-1)

Đường thẳng d' đi qua A(-4,2) và có vecto chỉ phương \(\overrightarrow{AM}\)(3,-3)\(\Rightarrow\)d' có vecto pháp tuyến n=(1,1) phương trình tổng quát của d' là: x+y+2=0

c) Gọi I(t,t+1)\(\in\Delta\)

Ta có \(\overrightarrow{IA}\)(-4-t,-t+1),\(\overrightarrow{IB}\left(-3-t,-t-3\right)\Rightarrow\overrightarrow{IA}+\overrightarrow{IB}=\left(-2t-7,-2t-2\right)\)

\(|\overrightarrow{IA}+\overrightarrow{IB}|=\sqrt{\left(-2t-7\right)^2+\left(-2t-2\right)^2}=\sqrt{8\left(t+\dfrac{9}{4}\right)^2+\dfrac{25}{2}}\ge\dfrac{5\sqrt{2}}{2}\forall t\inℝ\)

Dấu bằng xảy ra khi và chỉ khi t=\(-\dfrac{9}{4}\Rightarrow I\left(-\dfrac{9}{4},\dfrac{-4}{4}\right)\)

Answer 7

  

Answer 8

 

 

Answer 9

  
      

Answer 10

    

Answer 11

    

Answer 12

  

Answer 13

  

Answer 14

 

 

Answer 15

a) Đường thẳng $d$ đi qua $A(-4;2)$ và có vectơ pháp tuyến \overrightarrow{BC} =(4 ; 2)=2(2 ; 1)BC=(4;2)=2(2;1)

Ta có phương trình tổng quát của $d$ là: $2(x+4)+y-2=0\iff 2x+y+6=0$.

b) Vì S_{\triangle A M B}=S_{\Delta A MC}S△A MB​=SΔAMC​ suy ra $M$ là trung điểm của $BC$ $\Rightarrow M(-1;-1)$.

Đường thẳng d'd′ đi qua $A(-4;2)$ và có vectơ chỉ phương $\overrightarrow{}(3;-3)\Rightarrow$ d'd′ có vectơ pháp tuyến \vec{n}=(1 ; 1)n=(1;1)

Phương trình tổng quát của d'd′ là: $x+y+2=0$.

c) Gọi $I(t;t+1)\in \Delta$

Ta có \(\overrightarrow{IA}\left(-4-t;-t+1\right)\) , \(\overrightarrow{IB}\left(-3-t:-t-3\right)\) ⇒ \(\overrightarrow{IA}+\overrightarrow{IB}=\left(-2t-7;-2t-2\right)\)   \(\left|\overrightarrow{IA}+\overrightarrow{IB}\right|\)=\(\sqrt{\text{(−2t−7) ^2 +(−2t−2)^2 }}\)=\(\sqrt{\text{8t^2 +36t+53 }}\)=\(\sqrt{8\left(t+\dfrac{9}{4}\right)^2+\dfrac{25}{2}}\)\(\ge\)\(\dfrac{5\sqrt{2}}{2}\)∀t∈R

Dấu "=" khi và chỉ khi t=-\dfrac{9}{4} \Rightarrow I\left(-\dfrac{9}{4} ; \dfrac{-4}{4}\right)⇒t=\(-\dfrac{9}{4}\) ⇒I\(\left(-\dfrac{9}{4};\dfrac{-4}{4}\right)\)

 

 

 

Answer 16

a) đường thẳng d đi qua A(-4;2) và có vecto pháp tuyến BC =2(2;1)

=> Ta có phương trình tổng quát của d là : 2(x+4) + y-2=0 <=> 2x+y+6=0

b vì S tam giác AMB= S tam giác AMC => M là trung điểm của BC=> M (-1;-1)

Đường thẳng d' đi qua A(-4;2) và có vecto chỉ phương AM (3;-3) => d' có vecto pháp tuyến n= (1;1) 

Phương trình tổng quát  của d' là : x+y+2=0

c Gọi I(t;t+1) ϵ△

Ta có vecto IA (-4-t;-t+1).vecto IB(-3-t;-t-3)=> vecto IA +vecto IB=(-2t-7;-2t-2)

giá trị tuyệt đối vecto IA+ vecto IB = \(\sqrt{\left(-2t-7\right)^2_{ }+\left(-2t-2\right)^2}=\sqrt{8t^2}+36t+53=\sqrt{8\left(t+\dfrac{9}{4}\right)^2+\dfrac{25}{2}}\ge\dfrac{5\sqrt{2}}{2}\)

Dấu = xảy ra khi vào chỉ khi t= -9/4 => I(-9/4;-1)

Answer 17

Answer 18

 

Answer 19

Answer 20

    

Answer 21

    

Answer 22

 

 

Answer 23

    

Answer 24

 

Answer 25

    

Answer 26

 

Answer 27

    

Answer 28

 

Answer 29

 

Answer 30