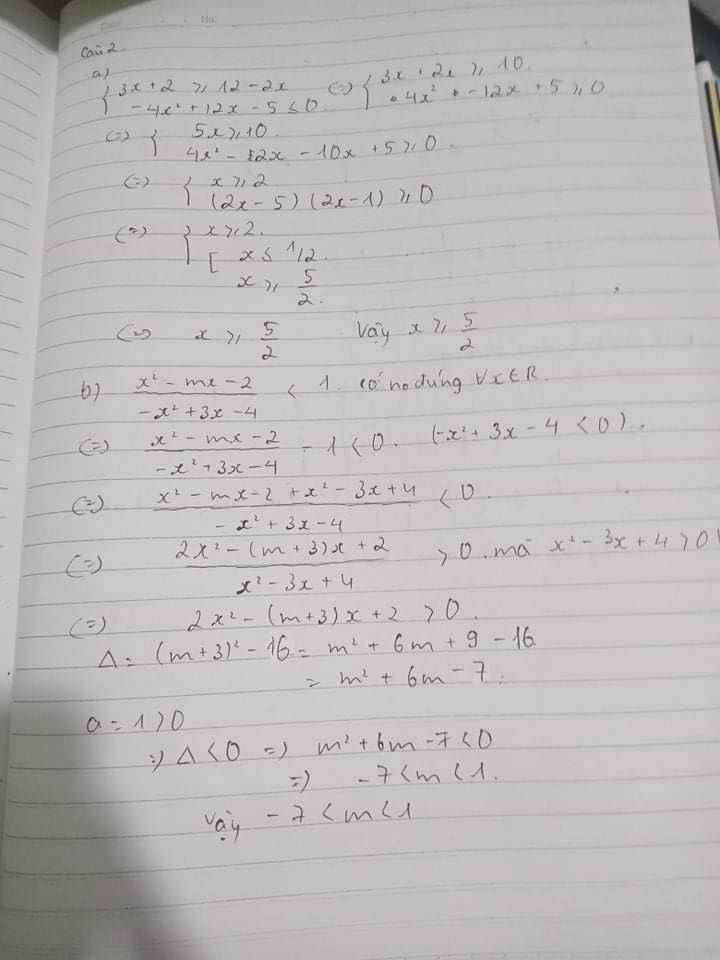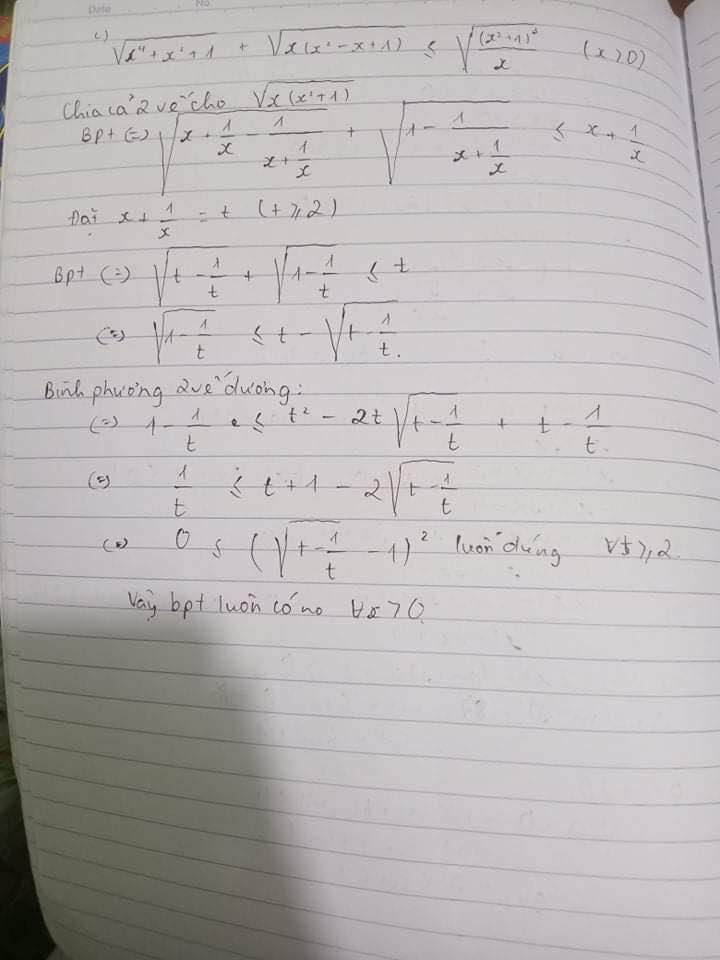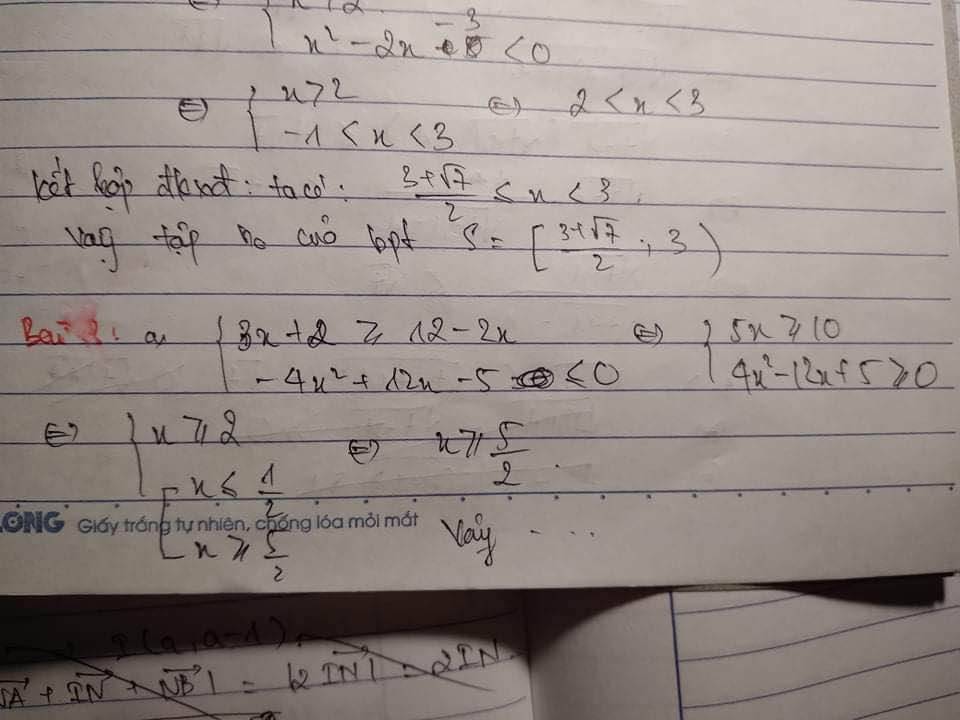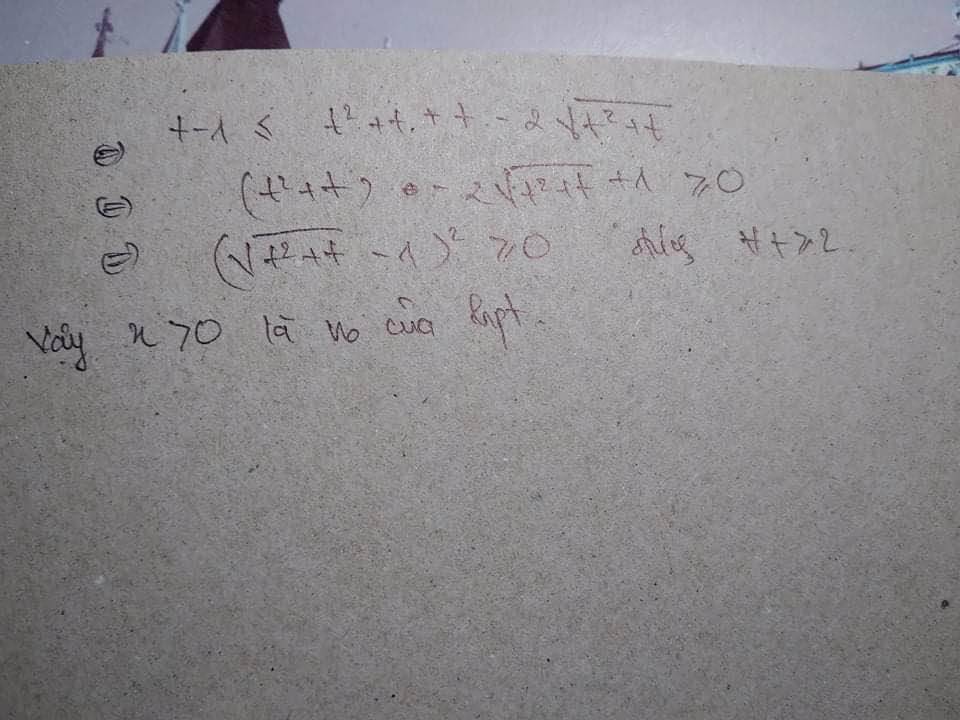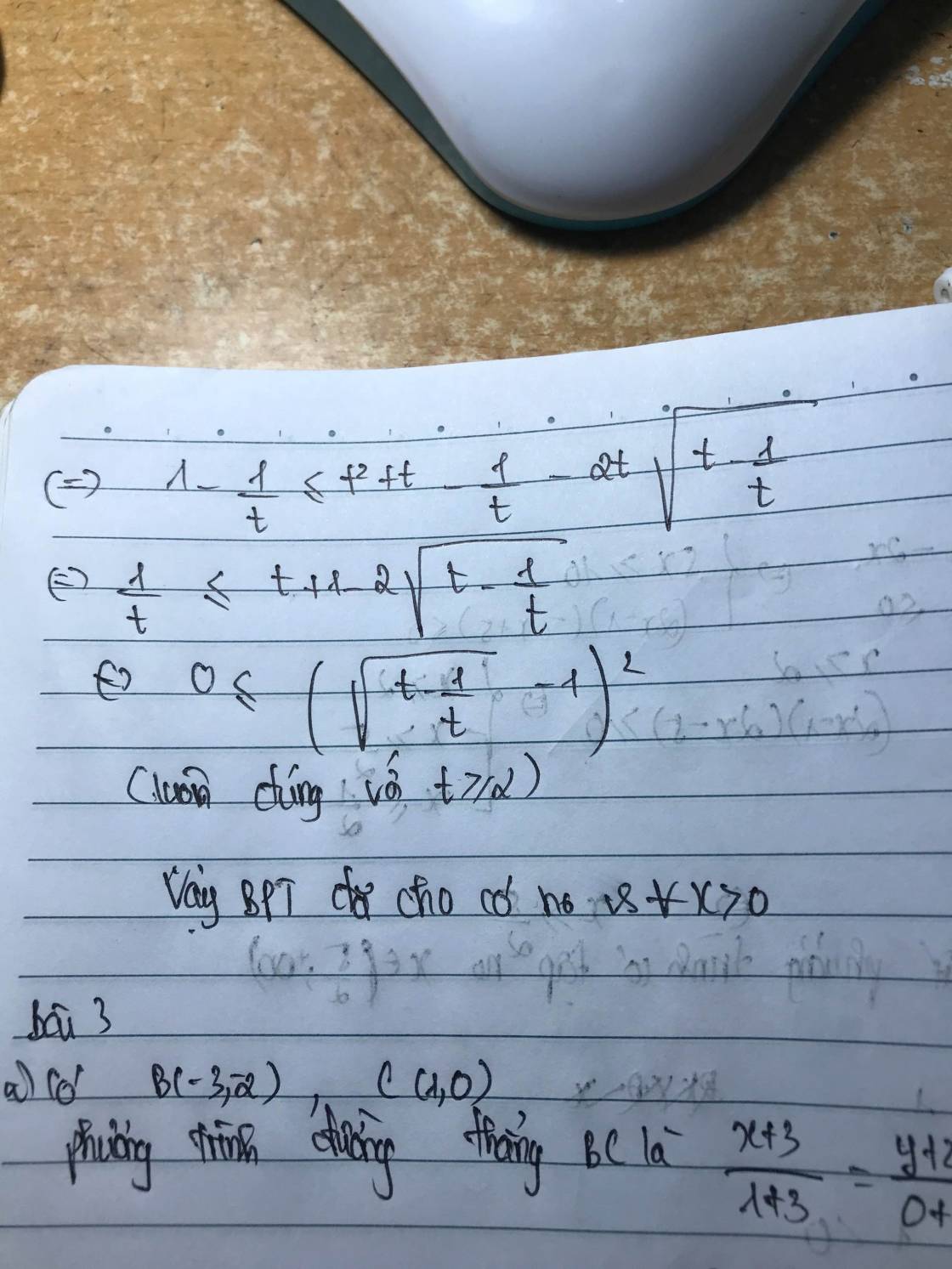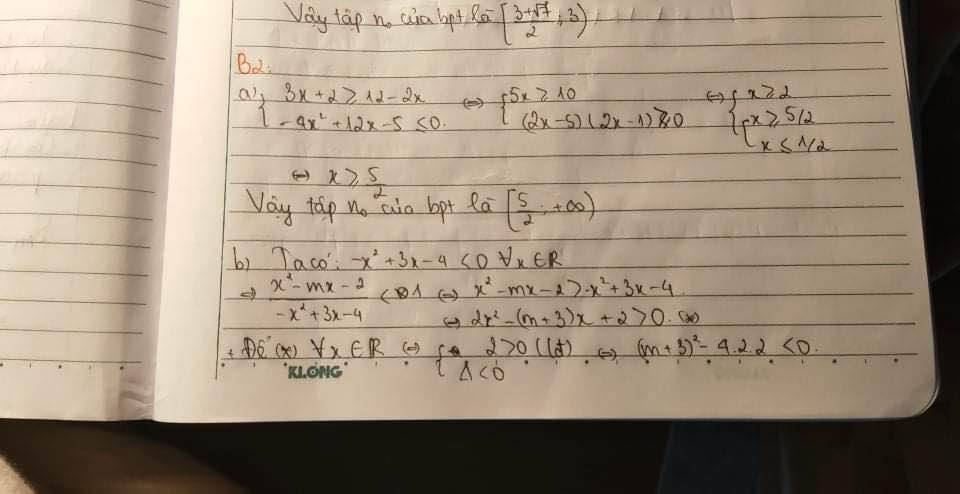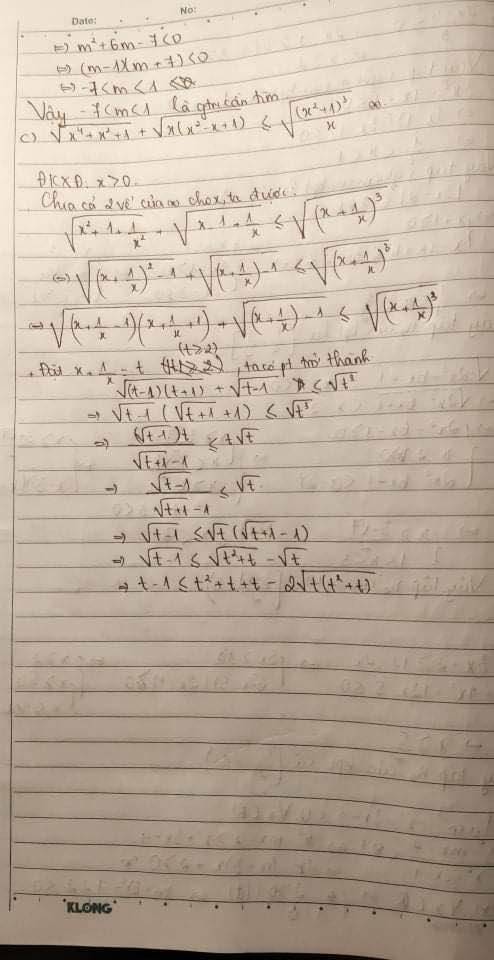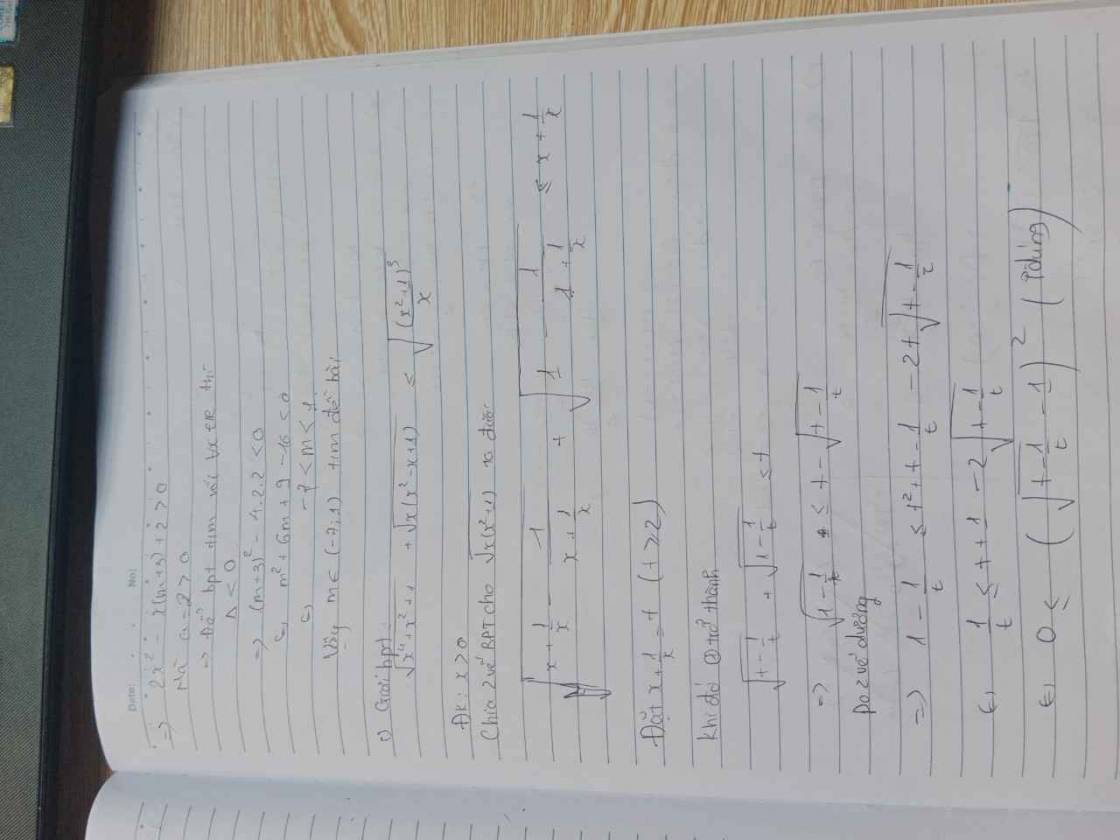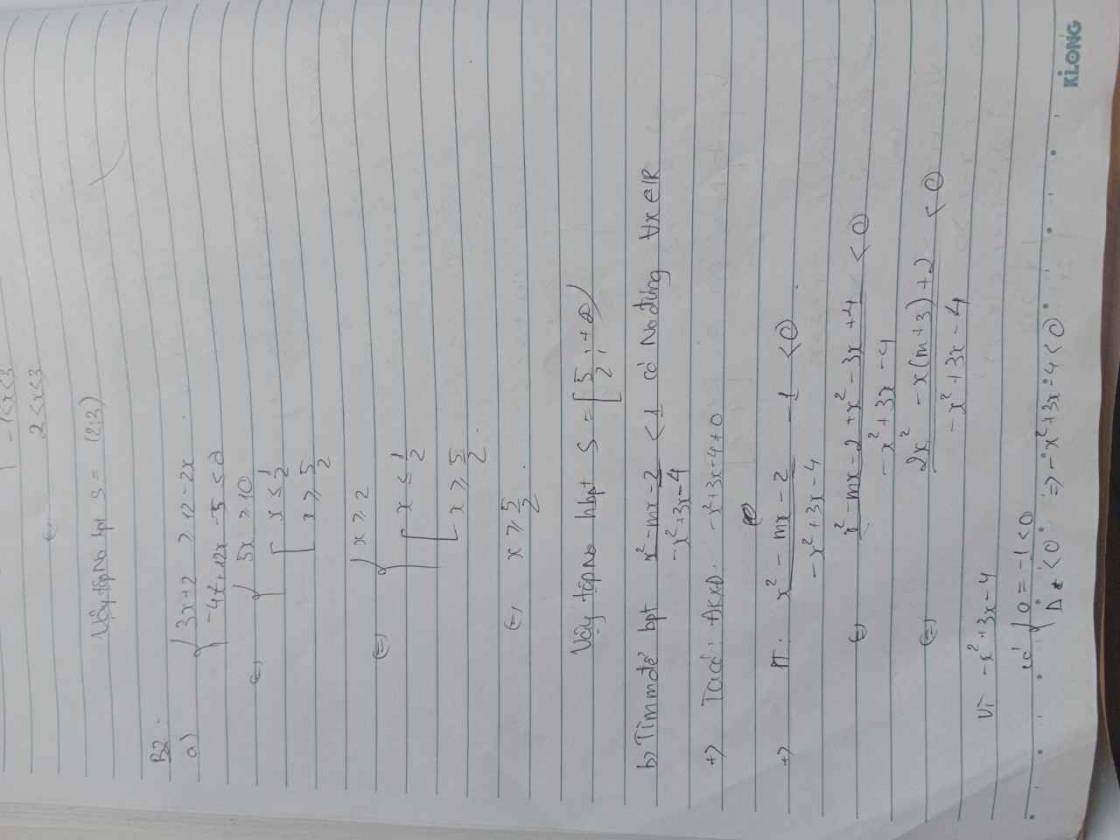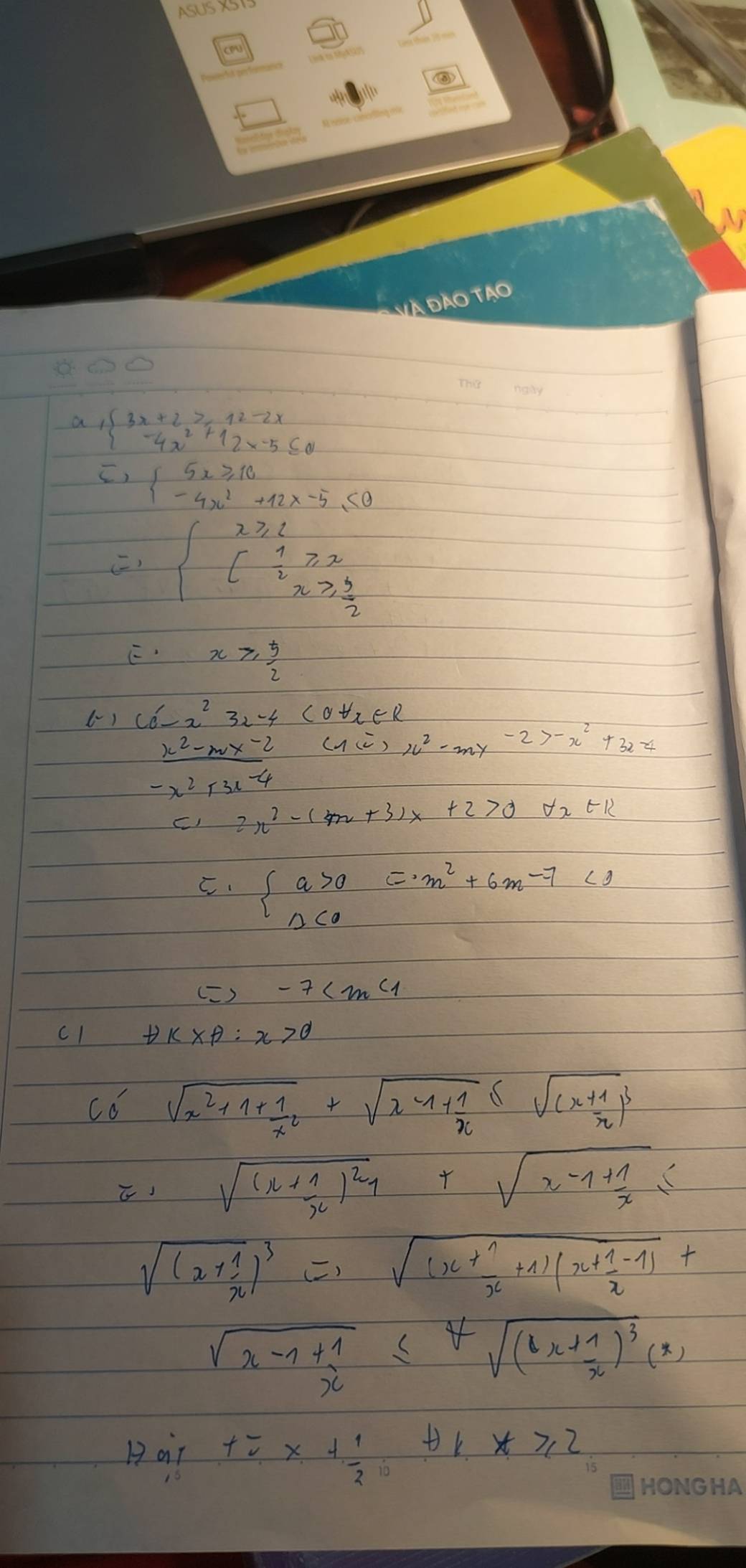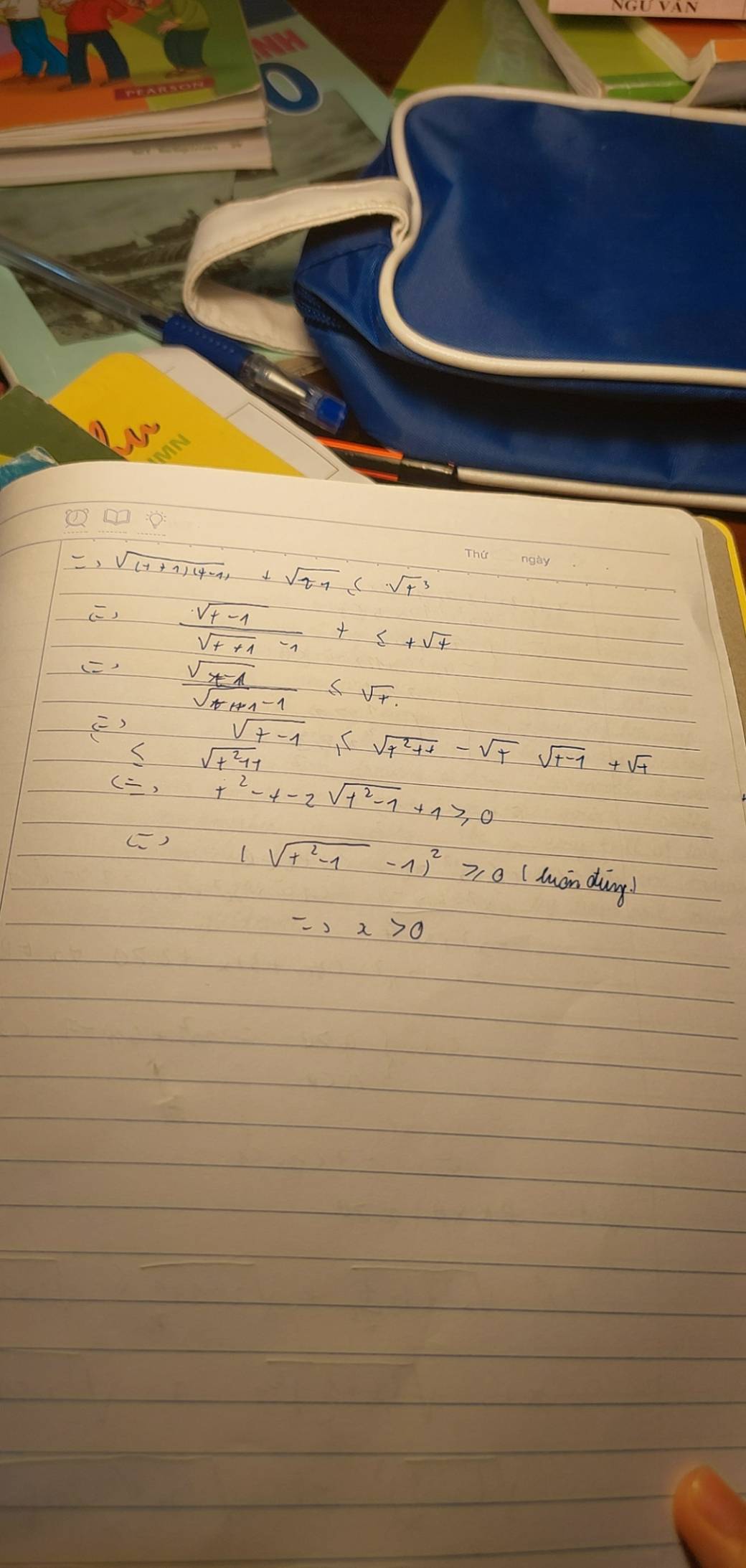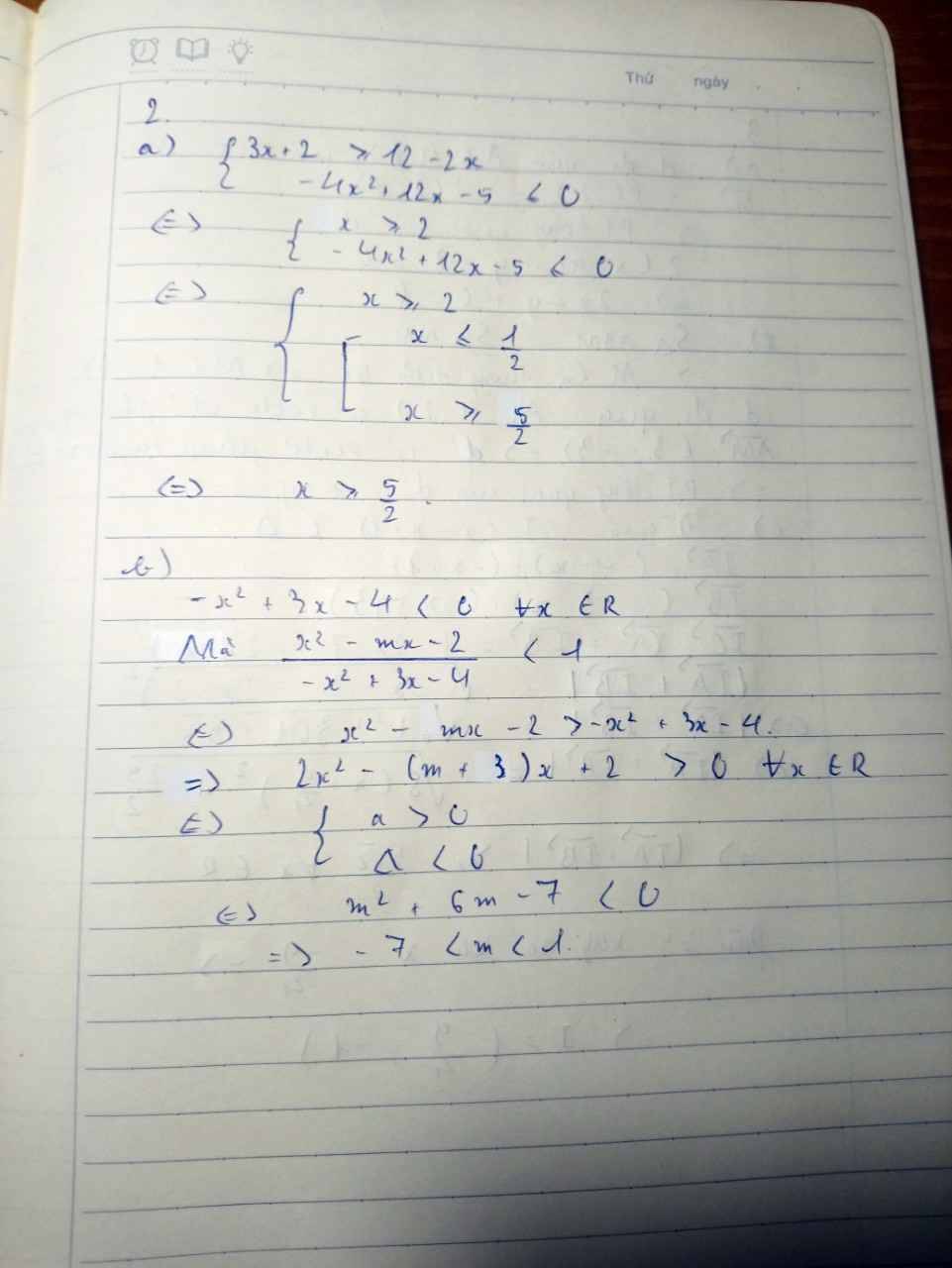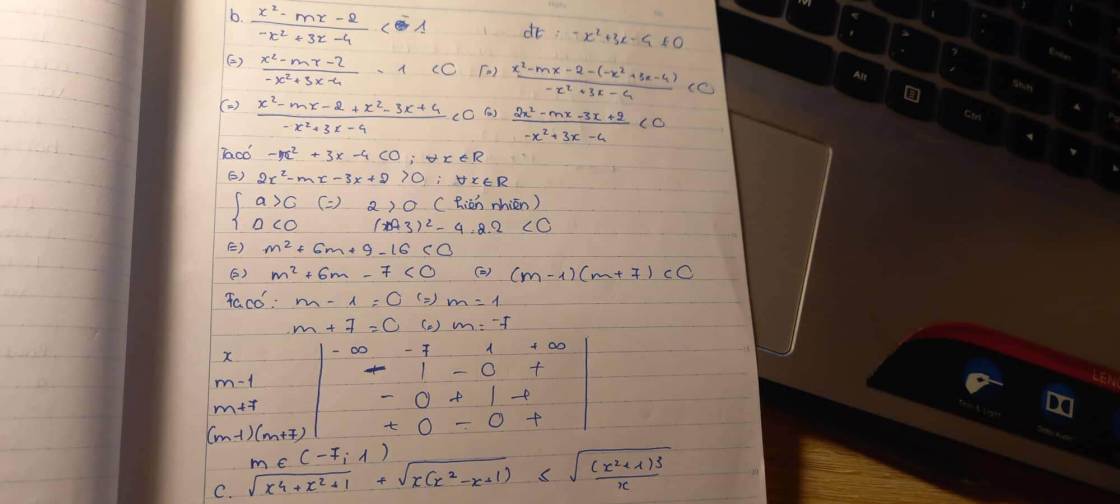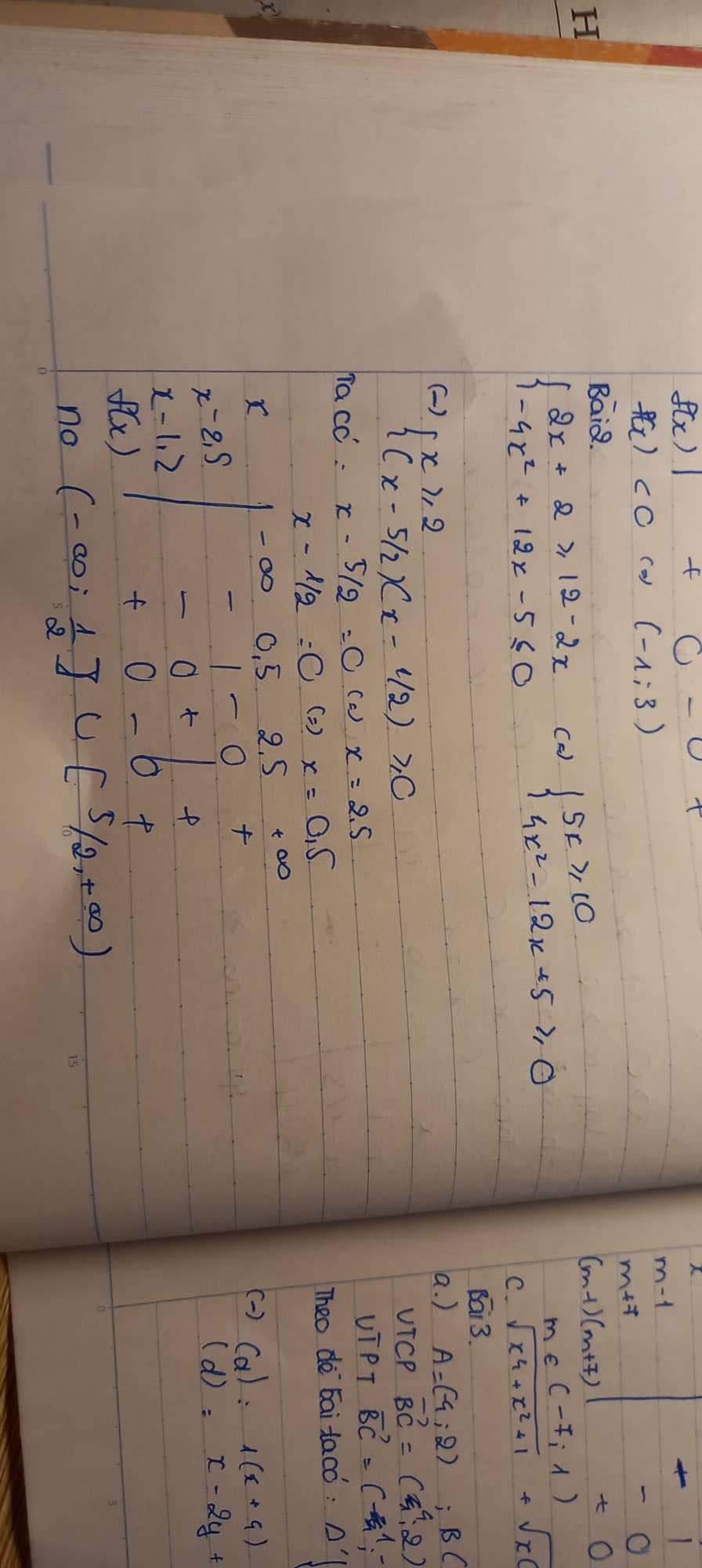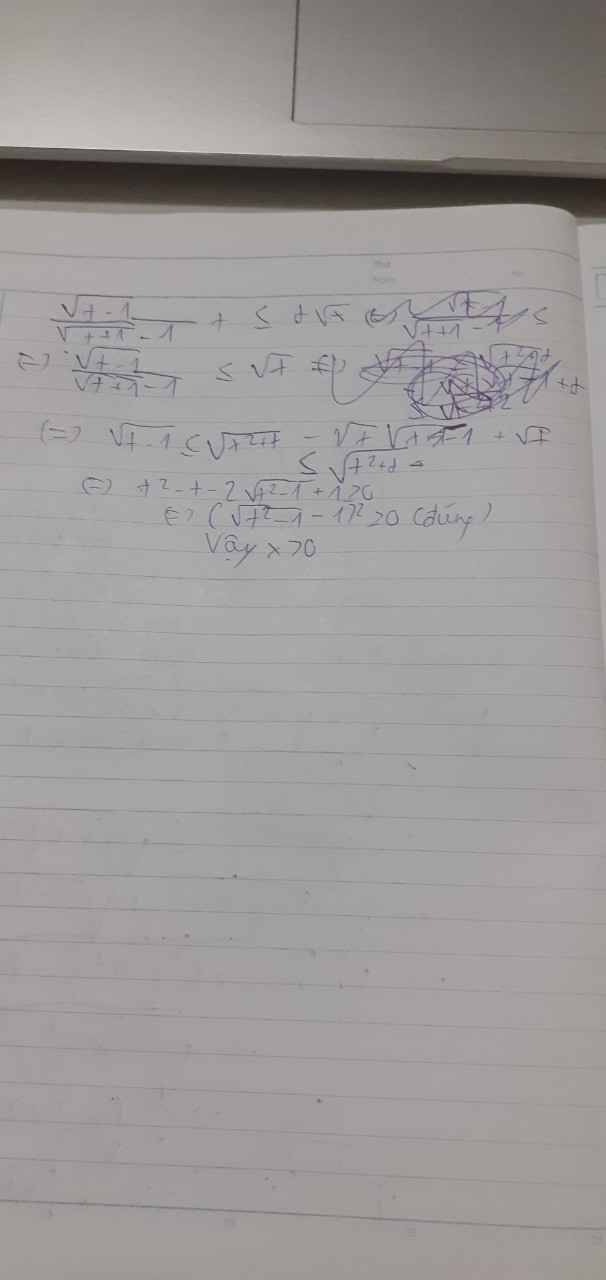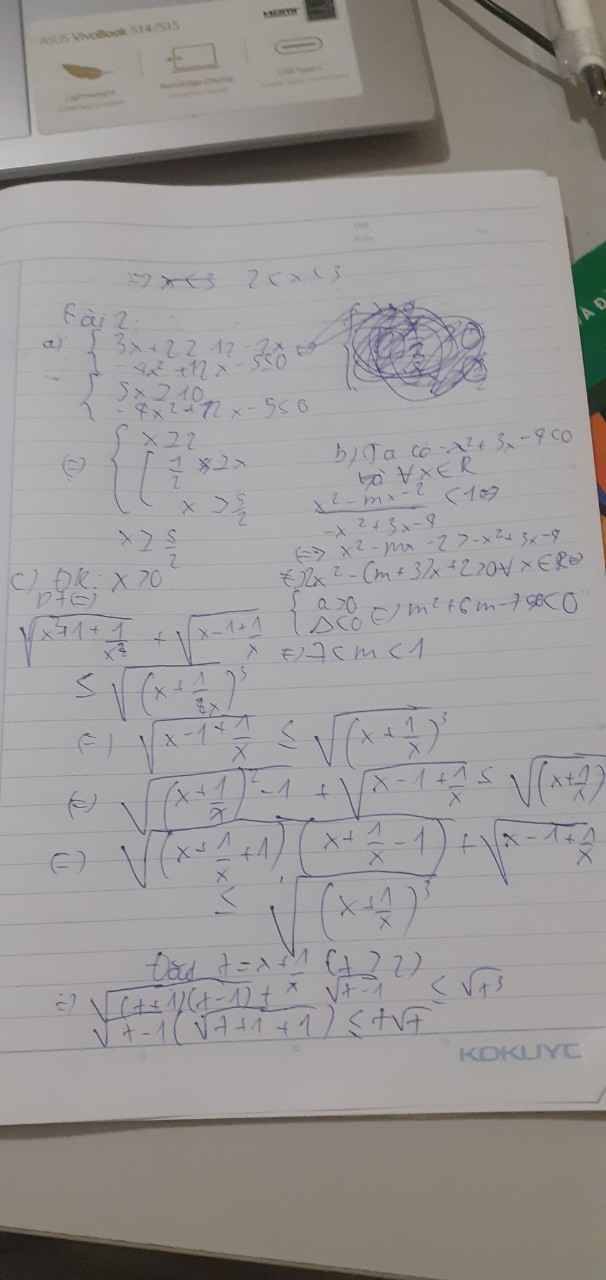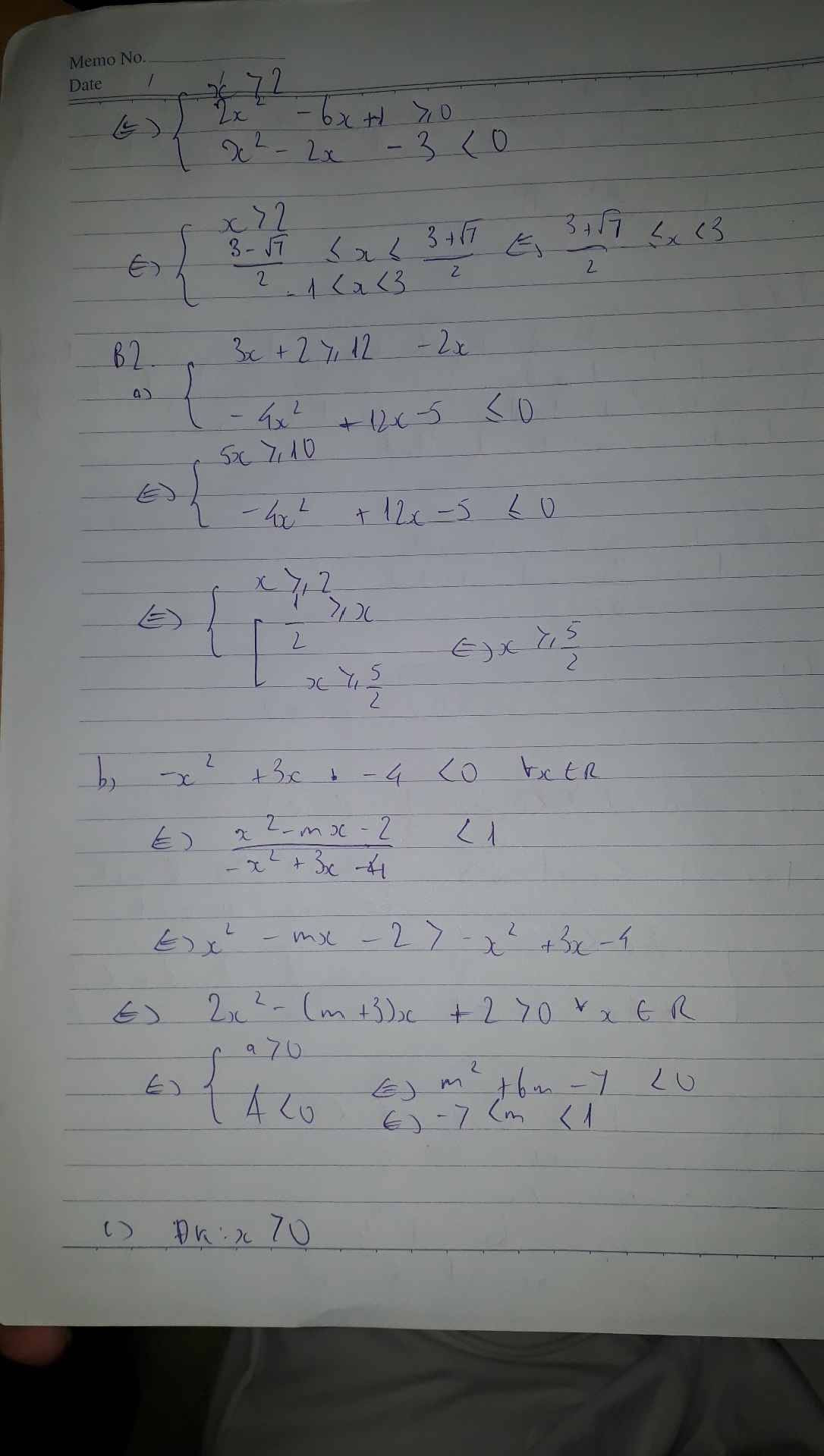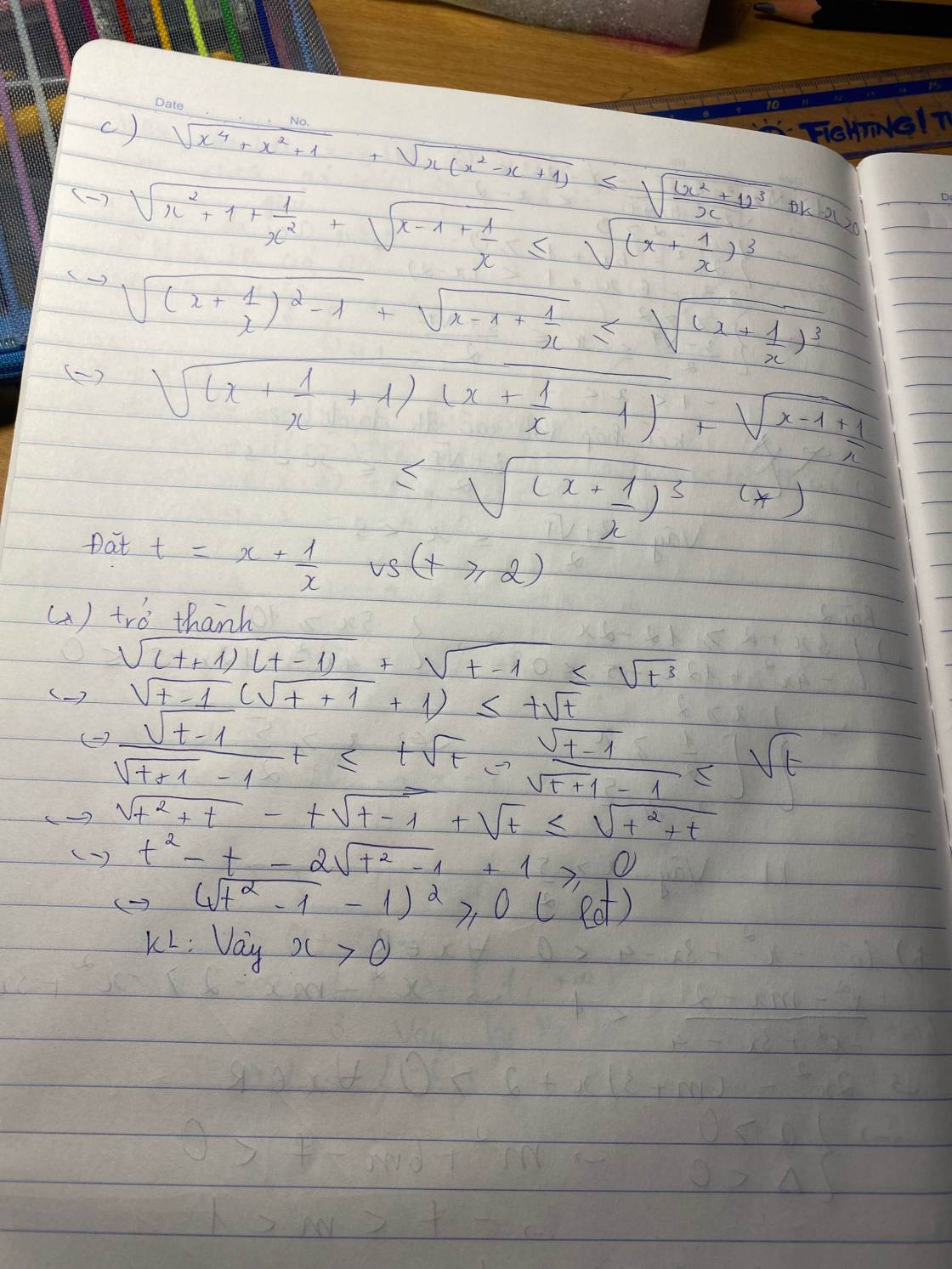Question

Câu 2 (3 diểm)

a) Giải hệ bất phương trình: $\left\{\begin{aligned} &3 x+2 \geq 12-2 x \\ &-4 x^{2}+12 x-5 \leq 0\end{aligned}\right.$

b) Tìm $m$ để bất phương trình $\dfrac{x^{2}-m x-2}{-x^{2}+3 x-4}<1$ có nghiệm đúng với mọi $x \in \mathbb{R}$.

c) Giải bất phương trình $\sqrt{x^{4}+x^{2}+1}+\sqrt{x\left(x^{2}-x+1\right)} \leq \sqrt{\dfrac{\left(x^{2}+1\right)^{3}}{x}}$.

Answer 1

  

Answer 2

Answer 3

    

Answer 4

Answer 5

Answer 6

Answer 7

    

Answer 8

a)\(\left\{{}\begin{matrix}3x+2\ge12-2x\\-4x^2+12x-5\le0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}5x\ge10\\-4x^2+12x-5\le0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge2\\\left[{}\begin{matrix}\dfrac{1}{2}\ge x\\x\ge\dfrac{5}{2}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow x\ge\dfrac{5}{2}\)

Answer 9

  

Answer 10

 

 

Answer 11

    

Answer 12

      

Answer 13

    

Answer 14

    

Answer 15

    

Answer 16

 

 

Answer 17

Answer 18

Answer 19

a)\(\left\{{}\begin{matrix}3x+2\ge12-2x\\-4x^2+12x-5\le0\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}5x\ge10\\-4x^2+12x-5\le0\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}x\ge2\\\left[{}\begin{matrix}\dfrac{1}{2}\ge x\\x\ge\dfrac{5}{2}\end{matrix}\right.\end{matrix}\right.\)⇔ x\(\ge\)\(\dfrac{5}{2}\)

b) Ta có -x^2 + 3x - 4 < 0−x2+3x−4<0 $\forall x\in \mathbb{R}$.

\(\dfrac{\text{x^2 −mx−2}}{-x^2+3x-4}< 1\)⇔x2−mx−2>−x2+3x−4

⇔2x2−(m+3)x+2>0∀x∈R⇔\(\left\{{}\begin{matrix}a>0\\\text{Δ< 0 ​ }\Delta< 0\end{matrix}\right.\)⇔\(^{^{^{ }}m^2}\)
+6m−7<0⇔−7<m<1.

c) Điều kiện $x>0$

Phương trình \Leftrightarrow⇔ \(\sqrt{x^2+1+\dfrac{1}{x^2}}+\sqrt{x-1+\dfrac{1}{x}}\le\sqrt{\left(x+\dfrac{1}{x}\right)^3}\) ⇔\(\sqrt{\left(x+\dfrac{1}{x}\right)^2-1}+\sqrt{x-1+\dfrac{1}{x}}\le\sqrt{\left(x+\dfrac{1}{x}\right)}\) ⇔\(\sqrt{\left(x+\dfrac{1}{x}+1\right)\left(x+\dfrac{1}{x}-1\right)}+\sqrt{x-1+\dfrac{1}{x}}\le\sqrt{\left(x+\dfrac{1}{x}\right)^3}\) *

Phương trình $(\ast )$ trở thành:

(t+1)(t−1)​+t−1​≤t3​⇔t−1​(t+1​+1)≤tt​⇔t+1​−1t−1​​t≤tt​⇔t+1​−1t−1​​≤t​⇔t−1​≤t2+t​−t​t−1​+t​≤t2+t​⇔t2−t−2t2−1​+1≥0⇔(t2−1​−1)2≥0 (đúng)

vậy x>0

Answer 20

 

Answer 21

Answer 22

      

Answer 23

    

Answer 24

 

 

Answer 25

 

 

Answer 26

    

Answer 27

 

Answer 28

    

Answer 29

 

 

 

Answer 30