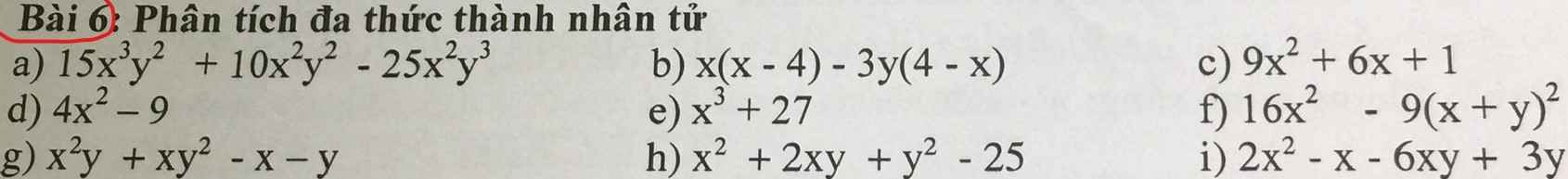Bài 1: Sử dụng hằng đẳng thức đáng nhớ:
\(A=(2x+3)[(2x)^2-2x.3+3^2]-2(4x^3-1)\)
\(=(2x)^3+3^3-(8x^3-2)=8x^3+27-8x^3+2=29\)
--------------
\(B=(x-1)^3-4x(x+1)(x-1)+3(x-1)(x^2+x+1)\)
\(=(x-1)[(x-1)^2-4x(x+1)+3(x^2+x+1)]\)
\(=(x-1)(x^2-2x+1-4x^2-4x+3x^2+3x+3)\)
\(=(x-1)(-3x+4)\)
Bài 2:
a)
\(x^2-y^2-3x+3y=(x^2-y^2)-(3x-3y)\)
\(=(x-y)(x+y)-3(x-y)=(x-y)(x+y-3)\)
b)
\((b-a)^2+(a-b)(3a-2b)-a^2+b^2\)
\(=(a-b)^2+(a-b)(3a-2b)-(a^2-b^2)\)
\(=(a-b)^2+(a-b)(3a-2b)-(a-b)(a+b)\)
\(=(a-b)[(a-b)+(3a-2b)-(a+b)]=(a-b)(3a-4b)\)
Bài 3:
\((2x-1)^2-(3x+4)^2=0\)
\(\Leftrightarrow [(2x-1)-(3x+4)][(2x-1)+(3x+4)]=0\)
\(\Leftrightarrow (-x-5)(5x+3)=0\Rightarrow \left[\begin{matrix} -x-5=0\\ 5x+3=0\end{matrix}\right.\Rightarrow \left[\begin{matrix} x=-5\\ x=-\frac{3}{5}\end{matrix}\right.\)
Vậy..........