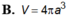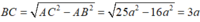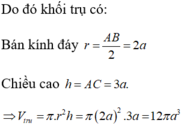Các câu hỏi tương tự
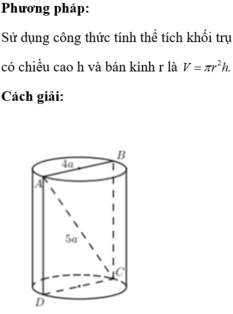
Cắt một khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có AB và CD thuộc hai đáy của hình trụ, AB4a, AC5a. Thể tích của khối trụ
Đọc tiếp
Cắt một khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có AB và CD thuộc hai đáy của hình trụ, AB=4a, AC=5a. Thể tích của khối trụ

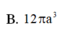
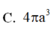
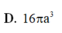
Cho khối trụ (T) có đường cao h, bán kính đáy R và h2R. Một mặt phẳng qua trục cắt khối trụ theo thiết diện là một hình chữ nhật có diện tích bằng
16
a
2
. Thể tích của khối trụ đã cho bằng
Đọc tiếp
Cho khối trụ (T) có đường cao h, bán kính đáy R và h=2R. Một mặt phẳng qua trục cắt khối trụ theo thiết diện là một hình chữ nhật có diện tích bằng 16 a 2 . Thể tích của khối trụ đã cho bằng
![]()
![]()
![]()
![]()
Khi cắt khối trụ (T) bởi một mặt phẳng qua trục của nó ta được thiết diện là một hình vuông có diện tích bằng
a
2
. Tính thể tích của khối trụ (T).
Đọc tiếp
Khi cắt khối trụ (T) bởi một mặt phẳng qua trục của nó ta được thiết diện là một hình vuông có diện tích bằng a 2 . Tính thể tích của khối trụ (T).
![]()
![]()
![]()
![]()
Cho hình trụ có bán kính đáy bằng
a
2
. Cắt hình trụ bởi một mặt phẳng, song song với trụ của hình trụ và cách trục của hình trụ một khoảng bằng
a
2
ta được thiết diện là một hình vuông. Tính thể tích V của khối trụ đã cho.
Đọc tiếp
Cho hình trụ có bán kính đáy bằng a 2 . Cắt hình trụ bởi một mặt phẳng, song song với trụ của hình trụ và cách trục của hình trụ một khoảng bằng a 2 ta được thiết diện là một hình vuông. Tính thể tích V của khối trụ đã cho.
![]()
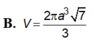
![]()
![]()
Khi cắt khối trụ (T) bởi một mặt phẳng qua trục của nó ta được thiết diện là một hình vuông có diện tích bằng
a
2
. Tính thể tích V của khối trụ (T).
Đọc tiếp
Khi cắt khối trụ (T) bởi một mặt phẳng qua trục của nó ta được thiết diện là một hình vuông có diện tích bằng a 2 . Tính thể tích V của khối trụ (T).
![]()
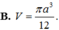
![]()
![]()
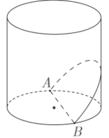
Cho khối trụ có bán kính đáy bằng 4(cm) và chiều cao 5(cm). Gọi AB là một dây cung đáy dưới sao cho AB
4
3
(cm). Người ta dựng mặt phẳng (P) đi qua hai điểm A, B và tạo với mặt phẳng đáy hình trụ một góc
60
°
như hình vẽ. Tính diện tích thiết diện của hình trụ cắt bởi mặt phẳng (P).
Đọc tiếp
Cho khối trụ có bán kính đáy bằng 4(cm) và chiều cao 5(cm). Gọi AB là một dây cung đáy dưới sao cho AB= 4 3 (cm). Người ta dựng mặt phẳng (P) đi qua hai điểm A, B và tạo với mặt phẳng đáy hình trụ một góc 60 ° như hình vẽ. Tính diện tích thiết diện của hình trụ cắt bởi mặt phẳng (P).
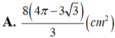
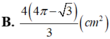
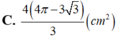
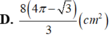
Cắt một khối trụ bởi một mặt phẳng vuông góc với trục của nó ta được thiết diện là một hình tròn có chu vi bằng chu vi vủa hình chữ nhật được tạo thành khi cắt mặt trụ bởi 1 mặt phẳng đi qua 2 tâm. Khi đó tỉ số
S
x
q
S
t
p
của khối trụ bằng:
Đọc tiếp
Cắt một khối trụ bởi một mặt phẳng vuông góc với trục của nó ta được thiết diện là một hình tròn có chu vi bằng chu vi vủa hình chữ nhật được tạo thành khi cắt mặt trụ bởi 1 mặt phẳng đi qua 2 tâm. Khi đó tỉ số S x q S t p của khối trụ bằng:
![]()
![]()
![]()
![]()
Cho hình trụ có bán kính đáy là Ra, mặt phẳng qua trục cắt hình trụ theo một thiết diện có diện tích bằng
8
a
2
. Diện tích xung quanh của hình trụ và thể tích khối trụ là:
Đọc tiếp
Cho hình trụ có bán kính đáy là R=a, mặt phẳng qua trục cắt hình trụ theo một thiết diện có diện tích bằng 8 a 2 . Diện tích xung quanh của hình trụ và thể tích khối trụ là:
![]()
![]()
![]()
![]()
Một hình trụ có bán kính đáy r5cm và khoảng cách giữa hai đáy h7cm. Cắt khối trụ bởi một mặt phẳng song song với trục và cách trụ 3cm. Diện tích của thiết diện được tạo thành là:
Đọc tiếp
Một hình trụ có bán kính đáy r=5cm và khoảng cách giữa hai đáy h=7cm. Cắt khối trụ bởi một mặt phẳng song song với trục và cách trụ 3cm. Diện tích của thiết diện được tạo thành là:
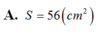
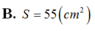
![]()
![]()