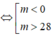Đáp án: B
Tam thức f(x) = x 2 - (m + 2)x + 8m + 1 đổi dấu hai lần khi và chỉ khi f(x) có hai nghiệm phân biệt
Ta có: Δ = [-(m + 2) ] 2 - 4.(8m + 1) = m 2 - 28m
f(x) có hai nghiệm phân biệt khi và chỉ khi
Δ > 0 ⇔
m
2
- 28m > 0