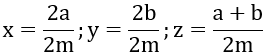Theo đề bài ta có 
(a, b, m ∈ Z; m > 0).
Quy đồng mẫu số các phân số ta được: 
Nhận xét: mẫu số 2m > 0 nên để so sánh x, y, z ta so sánh các tử số 2a, 2b, a+b.
Vì a < b nên a + a < b + a hay 2a < a + b.
Vì a < b nên a + b < b + b hay a + b < 2b.
Vậy ta có 2a < a+b < 2b nên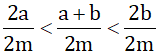 
hay x < z < y.
P/s : Đúng bài này không :> ?
Đề:
Giả sử (a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn 
thì ta có x < z < y.
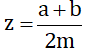
Giải:
x = \(\frac{a}{m}\)= \(\frac{2a}{2m}\)
y = \(\frac{b}{m}\)= \(\frac{2b}{2m}\)
Ta có: x < y => a < b (vì mẫu cùng bằng 2m)
a < b => a + a < a + b < b + b
<=> 2a < a + b < 2b
<=> \(\frac{2a}{2m}\)< \(\frac{a+b}{2m}\)< \(\frac{2b}{2m}\)
<=> x < z < y (đpcm)
