Các câu hỏi tương tự
Số phức z nào dưới đây là nghiệm phương trình (1+i) z 2 - ( 2 - i ) z ¯ + i - 2 = 0 ?
A. z = 4
B. z = 1 + i
C. z = -2i
D. z = 2 - i
Số phức za+bi, a,b thuộc R là nghiệm của phương trình
(
z
-
1
)
(
1
+
i
z
z
-
1
z
i
. Tổng Ta^2+b^2 bằng A. . B. . C. D. .
Đọc tiếp
Số phức z=a+bi, a,b thuộc R là nghiệm của phương trình ( z - 1 ) ( 1 + i z z - 1 z = i . Tổng T=a^2+b^2 bằng
A. ![]() .
.
B. ![]() .
.
C.![]()
D. ![]() .
.
Cho số phức z. Có bao nhiêu khẳng định sau là đúng? (*)
z
∈
ℝ
⇔
i
z
∉
ℝ
(*)
z
2
1
⇔
z
4
1
(*)
z
-
1
3
-
1
⇔
z
0
(*)
z...
Đọc tiếp
Cho số phức z. Có bao nhiêu khẳng định sau là đúng?
(*) z ∈ ℝ ⇔ i z ∉ ℝ
(*) z 2 = 1 ⇔ z 4 = 1
(*) z - 1 3 = - 1 ⇔ z = 0
(*) z + z ¯ = 0 ⇔ z = 0
A. 0
B. 1
C. 2
D. 3
Gọi z1; z2; z3; z4 là bốn nghiệm của phương trình ( z - 1 )( z + 2) ( z2 - 2z + 2) 0 trên tập số phức, tính tổng: A. 2/5 B. 3/5 C. 5/4 D. 6/7
Đọc tiếp
Gọi z1; z2; z3; z4 là bốn nghiệm của phương trình ( z - 1 )( z + 2) ( z2 - 2z + 2) = 0 trên tập số phức, tính tổng: 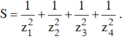
A. 2/5
B. 3/5
C. 5/4
D. 6/7
Cho số phức z thỏa mãn
z
-
1
+
i
2
Khẳng định nào sau đây là đúng?
Đọc tiếp
Cho số phức z thỏa mãn z - 1 + i = 2 Khẳng định nào sau đây là đúng?


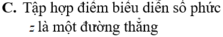
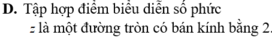
Cho số phức z = a + bi (với a,b là các số thực). Xét các phát biểu sau:
1:\(z^2-\overline{z}^2\) là số thực
2:\(z^2+\overline{z^2}\) là số ảo
3:\(z.\overline{z}\) là số thực
4:\(\left|z\right|-z\) bằng 0
Có bao nhiêu mệnh đề đúng?
A:0
B:1
C:2
D:3
Cho hai số phức z_1,z_2z1,z2. Biết rằng z_1+z_2z1+z2 và z_1.z_2z1.z2 là hai số thực. Chứng tỏ rằng z_1,z_2z1,z2 là hai nghiệm của một phương trình bậc hai với hệ số thực ?
Phương trình:
(
z
+
3
-
i
)
2
- 6(z + 3 - i) + 13 0 có 2 nghiệm phân biệt. Khẳng định nào sau đây là đúng? A. Trong 2 nghiệm có một nghiệm bằng 0. B. Cả 2 nghiệm đều là số thực. C. Cả 2 nghiệm đều là số thuần ảo. D. Trong 2 nghiệm có 1 nghiệm là số t...
Đọc tiếp
Phương trình: ( z + 3 - i ) 2 - 6(z + 3 - i) + 13 = 0 có 2 nghiệm phân biệt. Khẳng định nào sau đây là đúng?
A. Trong 2 nghiệm có một nghiệm bằng 0.
B. Cả 2 nghiệm đều là số thực.
C. Cả 2 nghiệm đều là số thuần ảo.
D. Trong 2 nghiệm có 1 nghiệm là số thực, 1 nghiệm là số thuần ảo.
Cho hai số phức z=(2x+3) + (3y-1)i và z'=3x + (y+1)i. Khi z=z', chọn khẳng định đúng.
![]()
![]()
![]()
![]()





