Từ giả thiết ta có x - 1 = 2 t
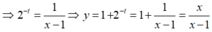
Chọn đáp án D.
Từ giả thiết ta có x - 1 = 2 t
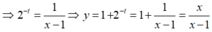
Chọn đáp án D.
Tính diện tích hình phẳng giới hạn bởi các đường sau:
a) y = 2x – x 2 , x + y = 2 ;
b) y = x 3 – 12x, y = x 2
c) x + y = 1, x + y = -1, x – y = 1, x – y = -1;
d) 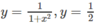
e) y = x 3 – 1 và tiếp tuyến với y = x 3 – 1 tại điểm (-1; -2).
Tiệm cận đứng và ngang của đồ thị hàm số sau là:
y = - 3 x - 2
A. x = 2, y = 0 B. x = 0, y = 2
C. x = 1, x = 1 D. x = -2; y = -3
Tiệm cận đứng và ngang của đồ thị hàm số sau là:
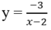
A. x = 2, y = 0 B. x = 0, y = 2
C. x = 1, x = 1 D. x = -2; y = -3
Hàm số nào sau đây không có cực trị
A: \(y=\dfrac{x^2+1}{x}\)
B: \(y=\dfrac{2x-x}{x+1}\)
C: \(y=x^2-2x+1\)
D: \(y=-x^3+x+1\)
Cho x,y,z,a,b,c là các số thực thay đổi thỏa mãn ( x + 3 ) 2 + ( y - 2 ) 2 + ( z + 1 ) 2 = 2 và a+b+c=1. Giá trị nhỏ nhất của biểu thức P = ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 là
A. 3 - 2
B. 3 + 2
C. 5 - 2 6
D. 5 + 2 6
Cho hàm số y = f ( x ) liên tục trên R \ { - 1 ; 0 } thỏa mãn f ( 1 ) = 2 ln 2 + 1 , x ( x + 1 ) f ' ( x ) + ( x + 2 ) f ( x ) = x ( x + 1 ) , ∀ x ∈ R \ { - 1 ; 0 } Biết f ( 2 ) = a + b ln 3 với a, b là hai số hữu tỉ. Tính T = a 2 - b
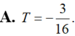
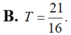
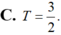
![]()
Trong không gian Oxyz, cho hai đường thẳng d: x = - 2 + 4 t y = 1 - 4 t z = - 2 + 3 t ; ∆ : x = - 2 + t ' y = 1 + n t ' z = - 2 + t ' và mặt phẳng (P): 2x-y+2z+1=0. Biết rằng ∆ song song với (P) và ∆ tạo với d một góc bé nhất, khi đó giá trị của biểu thức m 2 + n 2
A. 4.
B. 13.
C. 8.
D. 25.
trong các hàm số sau hàm số nào đồng biến trên R: A. y= 2x-1/x+2 B. y= -x^3+x^2-5x C. y= x^3+2x+1 D.-x^4-2x^2+3