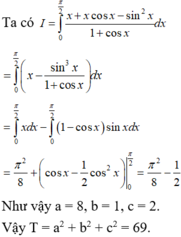Các câu hỏi tương tự
Cho biết
∫
0
1
x
2
.
e
x
(
x
+
2
)
2
d
x
a
b
e
+
c
với a,c là các số ngu...
Đọc tiếp
Cho biết ∫ 0 1 x 2 . e x ( x + 2 ) 2 d x = a b e + c với a,c là các số nguyên , b là số nguyên dương và a/b là phân số tối giản. Tính a-b+c
A. 3.
B. 0.
C. 2.
D. -3.
Cho f(x) là hàm liên tục trên đoạn [0;a] thỏa mãn
f
(
x
)
.
f
(
a
-
x
)
1...
Đọc tiếp
Cho f(x) là hàm liên tục trên đoạn [0;a] thỏa mãn f ( x ) . f ( a - x ) = 1 f ( x ) > 0 ; ∀ x ∈ [ 0 ; a ] và ∫ 0 a d x 1 + f ( x ) = b a c , trong đó b, c là hai số nguyên dương và b/c là phân số tối giản. Khi đó b+c có giá trị thuộc khoảng nào dưới đây?
A. (11;22)
B. (0;9)
C. (7;21)
D. (2017;2020)
hàm số
f
(
x
)
ln
1
-
1
x
2
. Biết rằng
f
(
2
)
+
F
(
3
)
+
.
.
.
+
f
(
2018
)
ln
a
-
ln
b...
Đọc tiếp
hàm số f ( x ) = ln 1 - 1 x 2 . Biết rằng f ( 2 ) + F ( 3 ) + . . . + f ( 2018 ) = ln a - ln b + ln c - ln d với a, b, c, d là các số nguyên dương, trong đó a, c, d là các số nguyên tố và a<b<c<d. Tính P=a+b+c+d
A. 1986
B. 1698
C. 1689
D. 1968
Biết
I
∫
0
4
x
ln
(
2
x
+
1
)
d
x
a
b
ln
3
-
c
, trong đó a, b, c là các số nguyên dương và a/b là phân số tối giản. Tính S a+b+c A. S 60 B. S 17 C. S 72 D. S 68
Đọc tiếp
Biết I = ∫ 0 4 x ln ( 2 x + 1 ) d x = a b ln 3 - c , trong đó a, b, c là các số nguyên dương và a/b là phân số tối giản. Tính S = a+b+c
A. S = 60
B. S = 17
C. S = 72
D. S = 68
Cho
∫
0
1
3
x
+
3
-
10
(
x
+
3
)
2
d
x
...
Đọc tiếp
Cho ∫ 0 1 3 x + 3 - 10 ( x + 3 ) 2 d x = 3 ln a b - 5 6 , trong đó a, b là 2 số nguyên dương và a/b là phân số tối giản. Mệnh đề nào dưới đây đúng?
A. ab = – 5
B. ab = 12
C. ab = 6
D. ab = 5/4
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?a) {y x + sinx, y x với 0
≤
x
≤
π
} và {y x + sinx, y x với
π
≤
x
≤
2
π
}b) {y sinx, y 0 với 0
≤
x
≤
π
} và {y cosx, y 0 với 0
≤
x
≤
π
};c) {y ...
Đọc tiếp
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?
a) {y = x + sinx, y = x với 0 ≤ x ≤ π } và {y = x + sinx, y = x với π ≤ x ≤ 2 π }
b) {y = sinx, y = 0 với 0 ≤ x ≤ π } và {y = cosx, y = 0 với 0 ≤ x ≤ π };
c) {y = x , y = x 2 }
và { y = 1 - x 2 , y = 1 − x}
Cho
∫
0
1
(
3
x
+
3
-
10
(
x
+
3
)
2
)
d
x
3
ln
a...
Đọc tiếp
Cho ∫ 0 1 ( 3 x + 3 - 10 ( x + 3 ) 2 ) d x = 3 ln a b - 5 6 , trong đó a, b là 2 số nguyên dương và a b là phân số tối giản. Mệnh đề nào dưới đây đúng ?
![]()
![]()
![]()
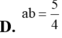
Thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi các đường: y
sin
2
/
3
x
, y 0 và x
π
/2 bằng:A. 1; B. 2/7;C. 2
π
; D. 2
π
/3.
Đọc tiếp
Thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi các đường: y = sin 2 / 3 x , y = 0 và x = π /2 bằng:
A. 1; B. 2/7;
C. 2 π ; D. 2 π /3.
Cho
∫
1
2
ln
x
(
x
+
1
)
2
d
x
a
b
ln
2
-
ln
c
với
a
,
b
,
c
là các số nguyên dương và...
Đọc tiếp
Cho ∫ 1 2 ln x ( x + 1 ) 2 d x = a b ln 2 - ln c với a , b , c là các số nguyên dương và a b là phân số tối giản. Tính giá trị của biểu thức S = a + b c

Cho hàm số yf(x) liên tục trên R và thỏa mãn f(x) + f(
π
3
-
x
)
1
2
sin
x
cos
x
(
8
cos
3
x
+
1
)
,
∀
x
∈...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và thỏa mãn f(x) + f( π 3 - x )= 1 2 sin x cos x ( 8 cos 3 x + 1 ) , ∀ x ∈ R Biết tích phân I= ∫ 0 π 3 f ( x ) d x được biểu diễn dưới dạng I= a b ln c d ; a , b , c , d ∈ Z và các phân số a b ; c d là các phân số tối giản. Tính S= a 3 + a b - c + d
![]()
![]()
![]()
![]()