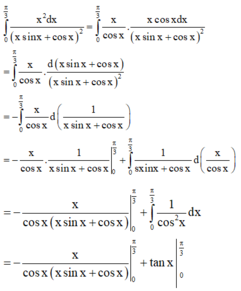
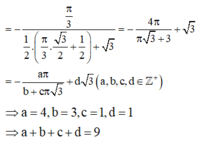Các câu hỏi tương tự
Thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi các đường: y
sin
2
/
3
x
, y 0 và x
π
/2 bằng:A. 1; B. 2/7;C. 2
π
; D. 2
π
/3.
Đọc tiếp
Thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi các đường: y = sin 2 / 3 x , y = 0 và x = π /2 bằng:
A. 1; B. 2/7;
C. 2 π ; D. 2 π /3.
Diện tích của hình phẳng được giới hạn bởi các đường: y = tanx; y = 0; x = -π/4 và x = π/4 bằng:
A. π; B. -π;
C. ln2; D. 0
Diện tích của hình phẳng được giới hạn bởi các đường: y = tanx; y = 0; x = - π /4 và x = π /4 bằng:
A. π ; B. - π ;
C. ln2; D. 0
Quay hình phẳng G giới hạn bởi các đường: y = x 3 ; y = 1, x = 0 xung quanh trục Oy. Khi đó thể tích của khối tròn xoay này bằng:
A. π B. 5 π /3
C. 3 π /5 D. 3/5
Cho hình phẳng giới hạn bởi các đường y=√x và y=x quay xung quanh trục Ox. Thể tích của khối tròn xoay tạo thành bằng:
(A). 0
(B). –π
(C). π
(D). π/6
Gọi VV là thể tích vật thể tròn CC xoay được tạo thành khi quay miền D được giới hạn bởi các đường yfleft(xright);y0;xa;xbyf(x);y0;xa;xb quanh trục OxOx. Khẳng định nào dưới đây đúng?Vint_a^bf^2left(xright)text{d}xV∫abf2(x)dx.Vpiint_a^bf^2left(xright)text{d}xVπ∫abf2(x)dx.Vpi^2int_a^bfleft(xright)text{d}x.Vπ2∫abf(x)dx.Vpiint_a^bfleft(xright)text{d}xVπ∫abf(x)dx.
Đọc tiếp
Gọi VV là thể tích vật thể tròn CC xoay được tạo thành khi quay miền D được giới hạn bởi các đường y=f\left(x\right);y=0;x=a;x=by=f(x);y=0;x=a;x=b quanh trục OxOx. Khẳng định nào dưới đây đúng?
V=\int_a^bf^2\left(x\right)\text{d}xV=∫abf2(x)dx.
V=\pi\int_a^bf^2\left(x\right)\text{d}xV=π∫abf2(x)dx.
V=\pi^2\int_a^bf\left(x\right)\text{d}x.V=π2∫abf(x)dx.
V=\pi\int_a^bf\left(x\right)\text{d}xV=π∫abf(x)dx.
Diện tích xung quanh của hình trụ có bán kính đáy a và đường cao a
3
là:A. 2
π
a
2
3
B. 2
π
a
2
C.
π
a
2
D.
π
a...
Đọc tiếp
Diện tích xung quanh của hình trụ có bán kính đáy a và đường cao a 3 là:
A. 2 π a 2 3 B. 2 π a 2
C. π a 2 D. π a 2 3
Thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi các đường: y = sin 2 / 3 x , y = 0 và x = π/2 bằng:
A. 1; B. 2/7;
C. 2π; D. 2π/3.
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:a) f(x)
(
25
-
x
2
)
trên đoạn [-4; 4]b) f(x) |
x
2
– 3x + 2| trên đoạn [-10; 10]c) f(x) 1/sinx trên đoạn [π/3; 5π/6]d) f(x) 2sinx + sin2x trên đoạn [0; 3π/2]
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) f(x) = ( 25 - x 2 ) trên đoạn [-4; 4]
b) f(x) = | x 2 – 3x + 2| trên đoạn [-10; 10]
c) f(x) = 1/sinx trên đoạn [π/3; 5π/6]
d) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
Một hình nón có đường kính đáy là 2a
π
3, góc ở đỉnh 120
°
. Thể tích của khối nón đó theo a là:A. 2
3
π
a
3
B. 3
π
a
3
C.
π
a
3
D.
π...
Đọc tiếp
Một hình nón có đường kính đáy là 2a π 3, góc ở đỉnh 120 ° . Thể tích của khối nón đó theo a là:
A. 2 3 π a 3 B. 3 π a 3
C. π a 3 D. π a 3 3