Chọn A
Đặt ![]()
Tập xác định: ![]()
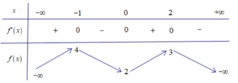
Xét hàm số trên đoạn [1;2]
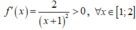 suy ra
suy ra 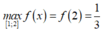
Bất phương trình
x
-
1
x
+
1
≥
m có nghiệm thuộc đoạn [1;2] khi và chỉ khi ![]()