Đáp án C
Phương pháp:
Dựa vào TCĐ và TCN của đồ thị hàm số.
Cách giải:
Đồ thị hàm số có TCĐ là x = 2 và TCN là y = 2
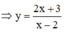
Đáp án C
Phương pháp:
Dựa vào TCĐ và TCN của đồ thị hàm số.
Cách giải:
Đồ thị hàm số có TCĐ là x = 2 và TCN là y = 2
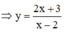
Cho hàm số y = f (x) có bảng biến thiên dưới đây:
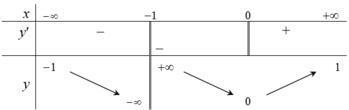
Hàm số y = f (x) có bảng biến thiên trên là hàm số nào dưới đây:
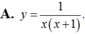
![]()
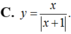
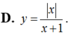
Hàm số y=(2x-1)/(x+1) có bảng biến thiên là bảng nào trong các bảng dưới đây
A. 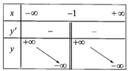
B. 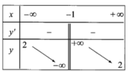
C. 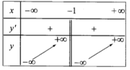
D. 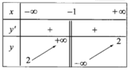
Cho hàm số y=f(x) với bảng biến thiên dưới đây.
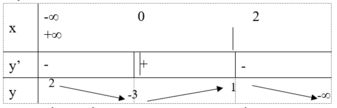
Trong số các kết luận sau, có bao nhiêu kết luận đúng?
(*) x C T = 0
(*) x C Đ = 2
(*) y m a x = 2
(*) TCN:y=2
(*) TCĐ là x = 0 và x = 2
A. 2
B. 3
C. 4
D. 5
Cho hàm số y = f(x) có bảng biến thiên như sau
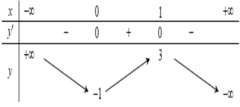
Hàm số y= f(x) đồng biến trên khoảng nào dưới đây?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y=f(x) có bảng biến thiên như sau:
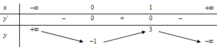
Hàm số y=f(x) đồng biến trên khoảng nào dưới đây?
![]()
![]()
![]()
![]()
Cho hàm số y = f(x) có bảng biến thiên như sau
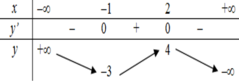
Hàm số y =f(x) đồng biến trên khoảng nào dưới đây?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y= f(x) có bảng biến thiên như hình sau
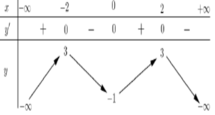
Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Hàm số y = f(x) có bảng biến thiên dưới đây.
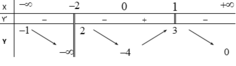
Số tiệm cận của đồ thị hàm số y = f(x) là:
A. 2
B. 3
C. 1
D. 4
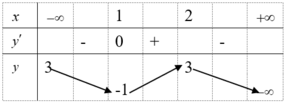
Hàm số y=f(x) có bảng biến thiên ở bên. Trong các phát biểu dưới đây có bao nhiêu phát biểu đúng?
(*): y = 3 là tiệm cận ngang
(*): Tập xác định D = ℝ / 2
(*): Max y = 3 (*): Min y = -1
(*): x C Đ = 2
![]()
![]()
![]()
![]()
Cho hàm số y=f(x) có đạo hàm liên tục trên i. Bảng biến thiên của hàm số y =f'(x) được cho như hình vẽ
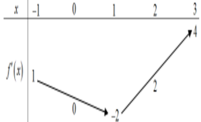
Hàm số y = f ( 1 - x 2 ) + x nghịch biến trên khoảng nào sau đây?
A. (-4;-2)
B. (-1; 1)
C. (1;3)
D. (-1;0)