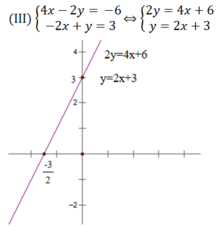
Hai đường thẳng trên trùng nhau nên hệ phương trình (III) có vô số nghiệm
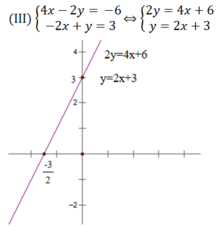
Hai đường thẳng trên trùng nhau nên hệ phương trình (III) có vô số nghiệm
Bằng minh họa hình học, hãy giải thích tại sao hệ (III) có vô số nghiệm.
(III) 4 x − 2 y = − 6 − 2 x + y = 3
Dựa vào minh họa hình học (xét vị trí tương đương đối của hai đường thẳng xác định bởi hai phương trình trong hệ) , em hãy giải thích các kết luận sau:
Hệ phương trình a x + b y = c a ' x + b ' y = c ' a , b , c , a ' , b ' , c ' khác 0
Có vô số nghiệm nếu a a ' = b b ' = c c '
Vô nghiệm nếu a a ' = b b ' ≠ c c '
Có một nghiệm duy nhất nếu a a ' ≠ b b '
Dựa vào minh họa hình học (xét vị trí tương đương đối của hai đường thẳng xác định bởi hai phương trình trong hệ) , em hãy giải thích các kết luận sau:
Hệ phương trình a x + b y = c a ' x + b ' y = c ' (a,b,c,a',b',c' khác 0)
- Có vô số nghiệm nếu a a ' = b b ' = c c ' ;
- Vô nghiệm nếu a a ' = b b ' ≠ c c ' ;
- Có một nghiệm duy nhất nếu a a ' ≠ b b '
Cho hệ phương trình I V 4 x + y = 2 8 x + 2 y = 1
Bằng minh họa hình học và phương pháp thế, chứng tỏ rằng hệ (IV) vô nghiệm.
1,Giải hệ \(\hept{\begin{cases}\sqrt{x^2+x+2}-\sqrt{x+y}=y\\\sqrt{x+y}=x-y+1\end{cases}}\)
2,Biết pt \(x^2-3x+1=0\)có nghiệm x=a
Hãy tìm 1 giá trị b nguyên để pt \(x^{16}-bx^8+1=0\)có nghiệm x = a
3, Cho hệ \(\left(I\right)\hept{\begin{cases}x+2y=m+3\\2x-3y=m\end{cases}}\)(m là tham số)
a, giải hệ với m = 1
b, tìm m để hệ (I) có nghiệm (x;y) sao cho \(P=98\left(x^2+y^2\right)+4m\)đạt GTNN
Cho hệ phương trình
(IV) 4 x + y = 2 8 x + 2 y = 1
Bằng minh họa hình học và phương pháp thế, chứng tỏ rằng hệ (IV) vô nghiệm.
hãy giải thích tại sao hệ phương trình sau có nghiệm duy nhất(mình đã giải hệ này rồi, chỉ cần giải thích)
Đáp số là:
x=2
y=0
Giải thích giúp mk vs
Cho các hệ phương trình sau:
a ) x = 2 2 x − y = 3 b ) x + 3 y = 2 2 y = 4
Trước hết, hãy đoán nhận số nghiệm của mỗi hệ phương trình trên (giải thích rõ lí do). Sau đó, tìm tập nghiệm của các hệ đã cho bằng cách vẽ hình.
Cho các hệ phương trình sau: x = 2 2 x - y = 3
Trước hết, hãy đoán nhận số nghiệm của mỗi hệ phương trình trên (giải thích rõ lí do). Sau đó, tìm tập nghiệm của các hệ đã cho bằng cách vẽ hình.