Chọn C
Từ bảng biến thiên của hàm số ta thấy: đồ thị hàm số có tiệm cận ngang là đường thẳng y = 1 nên loại đáp án A và B, hàm số ngịch biến trên mỗi khoảng 
nên 
loại dáp án D, vậy chọn C.
Cho hàm số y = f (x) có bảng biến thiên dưới đây:
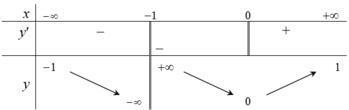
Hàm số y = f (x) có bảng biến thiên trên là hàm số nào dưới đây:
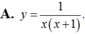
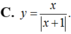
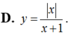
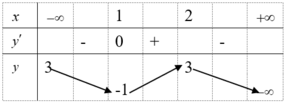
Hàm số y=f(x) có bảng biến thiên ở bên. Trong các phát biểu dưới đây có bao nhiêu phát biểu đúng?
(*): y = 3 là tiệm cận ngang
(*): Tập xác định D = ℝ / 2
(*): Max y = 3 (*): Min y = -1
(*): x C Đ = 2
Cho hàm số y= f(x) có bảng biến thiên như hình sau
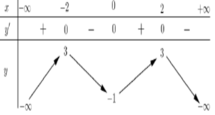
Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?
A. 
.
B. 
.
C. 
.
D. 
.
Cho hàm số y=f(x) với bảng biến thiên dưới đây.
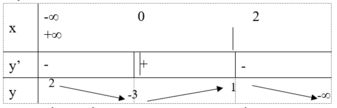
Trong số các kết luận sau, có bao nhiêu kết luận đúng?
(*) x C T = 0
(*) x C Đ = 2
(*) y m a x = 2
(*) TCN:y=2
(*) TCĐ là x = 0 và x = 2
A. 2
B. 3
C. 4
D. 5
Cho hàm số y = f(x) có bảng biến thiên như sau
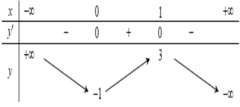
Hàm số y= f(x) đồng biến trên khoảng nào dưới đây?
A. 
.
B. 
.
C. 
.
D. 
.
Cho hàm số y=f(x) có bảng biến thiên như sau:
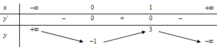
Hàm số y=f(x) đồng biến trên khoảng nào dưới đây?
Cho hàm số y = f(x) có bảng biến thiên như sau
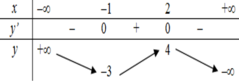
Hàm số y =f(x) đồng biến trên khoảng nào dưới đây?
A. 
B. 
C. 
D. 
Cho hàm số y=f(x) liên tục trên nửa khoảng [-1;2) có bảng biến thiên như hình vẽ. Khẳng định nào sau đây là đúng?
|
|
|
||
|
|
+ |
||
|
|
3 |
||
A.Không tồn tại giá trị nhỏ nhất của hàm số 
B.Hàm số nghịch biến trên khoảng 
C. 
D. Đường thẳng 
là tiệm cận đứng của đồ thị hàm số 
Hàm số y=(2x-1)/(x+1) có bảng biến thiên là bảng nào trong các bảng dưới đây
A.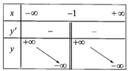 
B.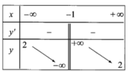 
C.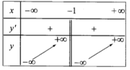 
D.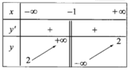 
Cho hàm số y=f(x) có bảng biến thiên như sau.
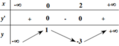
Hàm số y=f(x) đạt cực tiểu tại điểm nào trong các điểm được cho dưới đây?
A. x=2
B. x=-3
C. x=1
D. x=0
