\(a)x^2-x+\dfrac{1}{4}=0\\ \Leftrightarrow x^2-2.x.\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2=0\\ \Leftrightarrow\left(x-\dfrac{1}{2}\right)^2=0\\ \Leftrightarrow x-\dfrac{1}{2}=0\\ \Leftrightarrow x=\dfrac{1}{2}\)
\(b)x^2-\sqrt{2}=0\\ \Leftrightarrow x^2=\sqrt{2}\\ \Leftrightarrow x=\pm\sqrt{\sqrt{2}}\)
\(c)x^2+y^2-2x+4y+5=0\\ \Leftrightarrow\left(x^2-2x+1\right)+\left(y^2+4y+4\right)=0\\ \Leftrightarrow\left(x-1\right)^2+\left(y+2\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x-1=0\\y+2=0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
\(d)5x^2+9y^2-12xy-6x+9=0\\ \Leftrightarrow\left(x^2-6y+9\right)+\left(4x^2-12xy+9y^2\right)=0\\ \Leftrightarrow\left(x-3\right)^2+\left(2x-3y\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x-3=0\\2x-3y=0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=3\\2.3=3y\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=3\\y=2\end{matrix}\right.\)
a: \(\Leftrightarrow\left(x-\dfrac{1}{2}\right)^2=0\)
=>x-1/2=0
hay x=1/2
b: \(\Leftrightarrow x^2=\sqrt{2}\)
hay \(x=\pm\sqrt[4]{2}\)
c: \(\Leftrightarrow x^2-2x+1+y^2+4y+4=0\)
\(\Leftrightarrow\left(x-1\right)^2+\left(y+2\right)^2=0\)
=>x=1 và y=-2
d: \(\Leftrightarrow4x^2-12xy+9y^2+x^2-6x+9=0\)
\(\Leftrightarrow\left(x-3\right)^2+\left(2x-3y\right)^2=0\)
=>x=3 và 2x=3y
=>x=3 và y=2
a)\(x^2-x+\dfrac{1}{4}\)
\(\Leftrightarrow\left(x-\dfrac{1}{2}\right)^2=0\Leftrightarrow x=\dfrac{1}{2}\)
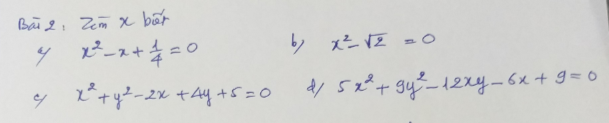
Bạn 
Các bn giải giúp mik nha , giải được bài nào thì giải ....@@@@
