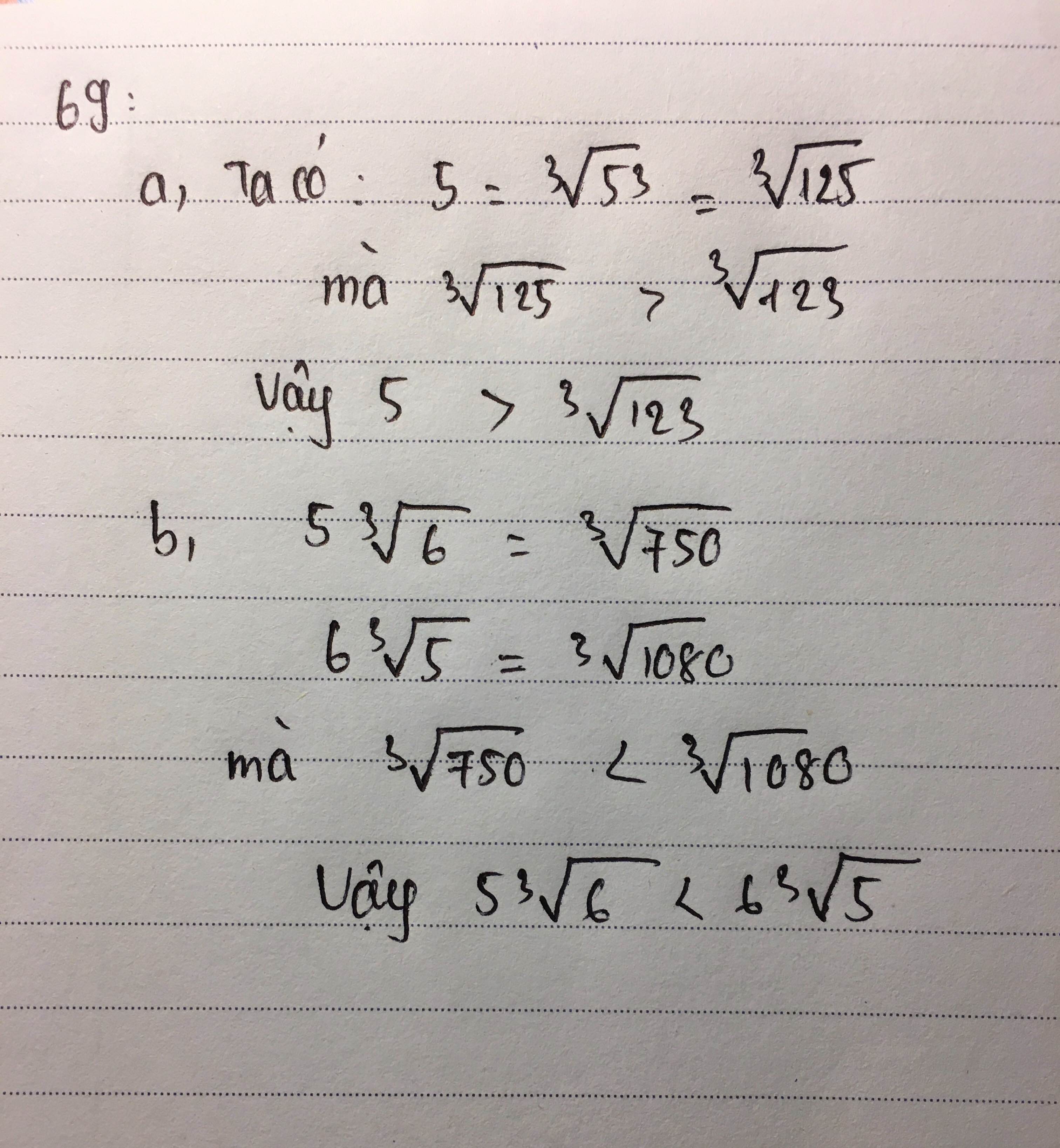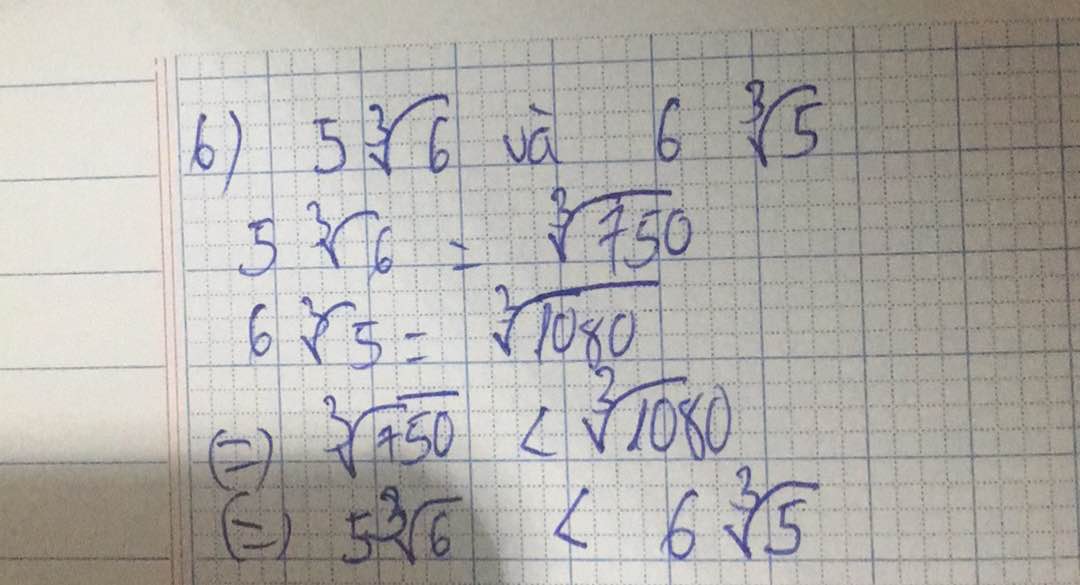a) mà suy ra .
b) Đưa về so sánh với . Kết quả .
) mà suy ra .
b) Đưa về so sánh với . Kết quả .
a) \(5=\sqrt[3]{125}>\sqrt[3]{123}\)
b) \(5\sqrt[3]{6}=\sqrt[3]{125.6}=\sqrt[3]{750};6\sqrt[3]{5}=\sqrt[3]{216.5}=\sqrt[3]{1080};\sqrt[3]{750}< \sqrt[3]{1080}\Rightarrow5\sqrt[3]{6}< 6\sqrt[3]{5}\)
a) mà suy ra .
b) Đưa về so sánh với . Kết quả .
a) Ta có: 5 = ∛53 = ∛125
Vì ∛125 > ∛123 nên 5 > ∛123
b) Ta có: 5∛6 = ∛53.6 = ∛125.6 = ∛750
6∛5 = ∛63.5 = ∛216.5 = ∛1080
Vì ∛750 < ∛1080 nên 5∛6 < 6∛5
a, Ta có:
\(5=\sqrt[3]{125}\\ \Leftrightarrow125>123\\ \Leftrightarrow\sqrt[3]{125}>\sqrt[3]{123}\\\Rightarrow5>\sqrt[3]{123}\)
b, Ta có:
\(5\sqrt[3]{6}=\sqrt[3]{750}\\6\sqrt[3]{5}=\sqrt[3]{1080}\\ \Leftrightarrow750< 1080\\ \Leftrightarrow\sqrt[3]{750}< \sqrt[3]{1080}\\ \Rightarrow5\sqrt[3]{6}< 6\sqrt[3]{5}\)
a) \(5=\sqrt[3]{5^3}=\sqrt[3]{125}>\sqrt[3]{123}\Rightarrow5>\sqrt[3]{123}\)
b) \(5\sqrt[3]{6}=\sqrt[3]{5^3\cdot6}=\sqrt[3]{750}\)
\(6\sqrt[3]{5}=\sqrt[3]{6^3\cdot5}=\sqrt[3]{1080}\)
Mà \(\sqrt[3]{750}< \sqrt[3]{1080}\Rightarrow5\sqrt[3]{6}< 6\sqrt[3]{5}\)
\(a,Ta\) \(có\): \(5=\sqrt[3]{5^3}=\sqrt[3]{125}\)
Vì \(125>123\) nên \(\sqrt[3]{125}>\sqrt[3]{123}\Leftrightarrow5>\sqrt[3]{123}\)
Vậy \(5>\sqrt[3]{123}\)
\(b,Ta\) \(có\): \(5\sqrt[3]{6}=\sqrt[3]{5^3.6}=\sqrt[3]{750}\)
\(6\sqrt[3]{5}=\sqrt[3]{6^3.5}=\sqrt[3]{1080}\)
\(Vì\) \(750< 1080\Leftrightarrow\sqrt[3]{750}< \sqrt[3]{1080}\)
\(\Leftrightarrow5\sqrt[3]{6}< 6\sqrt[3]{5}\)
Vậy \(5\sqrt[3]{6}< 6\sqrt[3]{5}\)
5 và \(\sqrt[3]{125}\) mà 5 =\(\sqrt[3]{125}\) vậy \(\sqrt[3]{125}\) >\(\sqrt[3]{123}\) suy ra 5>\(\sqrt[3]{123}\)
\(5\sqrt[3]{6}\) và \(6\sqrt[3]{5}\) mà\(\sqrt[3]{5^3\cdot6}\) =\(\sqrt[3]{750}\) và \(\sqrt[3]{5\cdot6^3}=\sqrt[3]{1080}\) vậy \(\sqrt[3]{750}\) <\(\sqrt[3]{1080}\)suy ra \(5\sqrt[3]{6}\)<\(6\sqrt[3]{5}\)
a)Ta có: \(5=\sqrt[3]{5^3}=\sqrt[3]{125}\)
Vì \(\sqrt[3]{125}>\sqrt[3]{123}\) nên \(5>\sqrt[3]{123}\)
b) Ta có: \(5\sqrt[3]{6}=\sqrt[3]{5^3.6}=\sqrt[3]{750}\); \(6\sqrt[3]{5}=\sqrt[3]{6^3.5}=\sqrt[3]{1080}\)
Vì \(\sqrt[3]{750}< \sqrt[3]{1080}\) nên \(5\sqrt[3]{6}< 6\sqrt[3]{5}\)
a. Ta có: \(5=\sqrt[3]{125}\)
Vì \(\sqrt[3]{125}>\sqrt[3]{123}\) nên \(5>\sqrt[3]{123}\)
b. Ta có: \(5\sqrt[3]{6}=\sqrt[3]{5^2.6}=\sqrt[3]{150}\approx5,3\)
\(6\sqrt[3]{5}=\sqrt[3]{6^2.5}=\sqrt[3]{180}\approx5,6\)
Vì 5,3<5,6 nên \(5\sqrt[3]{6}< 6\sqrt[3]{5}\)
a/5=\(^3\sqrt{125}\)⇔\(^3\sqrt{125}\)>\(^3\sqrt{123}\)⇒5>\(^3\sqrt{123}\)
b/\(5\sqrt[3]{6}=^3\sqrt{5^3.6}=750\)
\(6\sqrt[3]{5}=\sqrt[3]{6^3.5}=1080\)
⇔1080>750
⇒\(6\sqrt[3]{5}\)>\(5\sqrt[3]{6}\)
\(|5=\sqrt[3]{125}ma\sqrt[3]{125}>\sqrt[3]{123}\Rightarrow5>\sqrt[3]{123}|5.\sqrt[3]{6}va6.\sqrt[3]{5}taco5^3.6< 6^3.5\Rightarrow6.\sqrt[3]{5}>5.\sqrt[3]{6}\)
5> Căn bậc ba cảu 123
6Căn bậc ba của>5 căn bậc ba của6
) mà suy ra .
b) Đưa về so sánh với . Kết quả .
a)5>\(\sqrt[3]{123}\)
b)\(5\sqrt[3]{6}\)<\(6\sqrt[3]{5}\)
a) Ta có:\(5=\sqrt[3]{5^3=\sqrt[3]{125}}\)
Vì 125 > 123 ⇔ \(\sqrt[3]{125}>\sqrt[3]{123}\) ⇔ 5 > \(\sqrt[3]{123}\)
Vậy 5 >\(\sqrt[3]{123}\)
b) Ta có: \(5\sqrt[3]{6}=\sqrt[3]{5^3.6}=\sqrt[3]{125.6}=\sqrt[3]{750}\)
\(6\sqrt[3]{5}=\sqrt[3]{6^3.5}=\sqrt[3]{216.5}=\sqrt[3]{1080}\)
Vì 750 < 1080 ⇔ \(\sqrt[3]{750}< \sqrt[3]{1080}\) ⇔ \(5\sqrt[3]{6< 6\sqrt[3]{5}}\)
Vậy \(5\sqrt[3]{6}< 6\sqrt[3]{5}\)
a, Ta có \(125>123\) nên \(\sqrt[3]{125}>\sqrt[3]{123}\) hay \(5>\sqrt[3]{123}\)
b,Ta có 750<1080 hay \(5^3\cdot6< 6^3\cdot5\) <=> \(\sqrt[3]{5^3\cdot6}< \sqrt[3]{6^3\cdot5}\) <=>\(5\sqrt[3]{6}< 6\sqrt[3]{5}\)
a 5 và \(\sqrt[3]{123}\)
mà \(5=\sqrt[3]{125}\) ,\(\sqrt[3]{125}>\sqrt[3]{123}\)
nên 5>\(\sqrt[3]{123}\)
b 5\(\sqrt[3]{6}\) và 6\(\sqrt[3]{5}\)
mà \(5\sqrt[3]{6}=5^3.6;6\sqrt[3]{5}=6^3.5\)
\(\Leftrightarrow5^3.6< 6^3.5\)
nên\(5\sqrt[3]{6}< 6\sqrt[3]{5}\)
a) \(\sqrt[3]{123}\)\(\approx\)4,98
vì 5>4,9 nên 5>\(\sqrt[3]{123}\)
vậy 5>\(\sqrt[3]{123}\)
b) \(5\sqrt[3]{6}\)=\(\sqrt[3]{5^2\cdot6}\)=\(\sqrt[3]{25\cdot6}\)=\(\sqrt[3]{150}\)\(\approx\)5,31
\(6\sqrt[3]{5}\)=\(\sqrt[3]{6^2\cdot5}\)=\(\sqrt[3]{36\cdot5}\)=\(\sqrt[3]{180}\)\(\approx\)5,64
vì 5,31<5,64 nên \(5\sqrt[3]{6}\)<\(6\sqrt[3]{5}\)
vậy \(5\sqrt[3]{6}\)<\(6\sqrt[3]{5}\)
a)Ta có:5=\(\sqrt[3]{125}\)
125>123 =>\(\sqrt[3]{125}>\sqrt[3]{123}=>5>\sqrt[3]{123}\)
b)5\(\sqrt[3]{6}=\sqrt[3]{125}\sqrt[3]{6}=\sqrt[3]{125.6}=\sqrt[3]{750}\) (1)
6\(\sqrt[3]{5}=\sqrt[3]{216}.\sqrt[3]{5}=\sqrt[3]{216.5}=\sqrt[3]{1080}\left(2\right)\)
Từ (1),(2) suy ra 5\(\sqrt[3]{6}< 6\sqrt[3]{5}\)