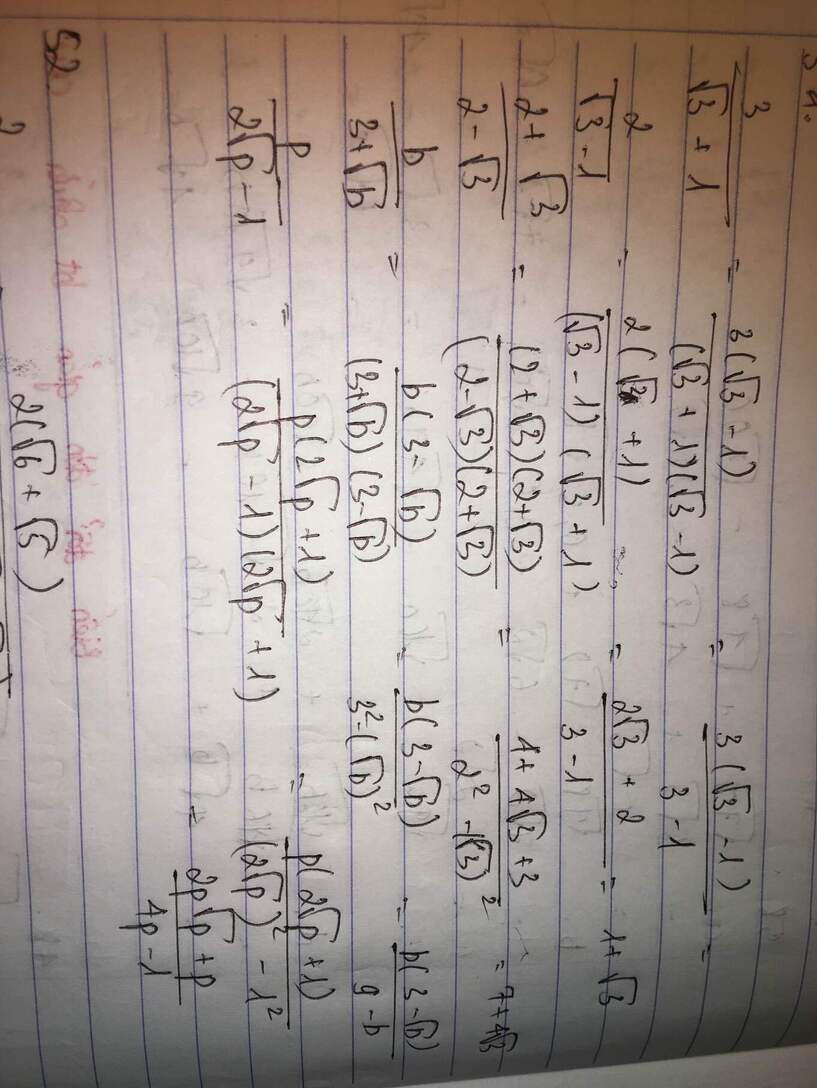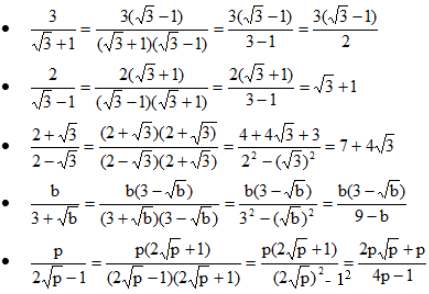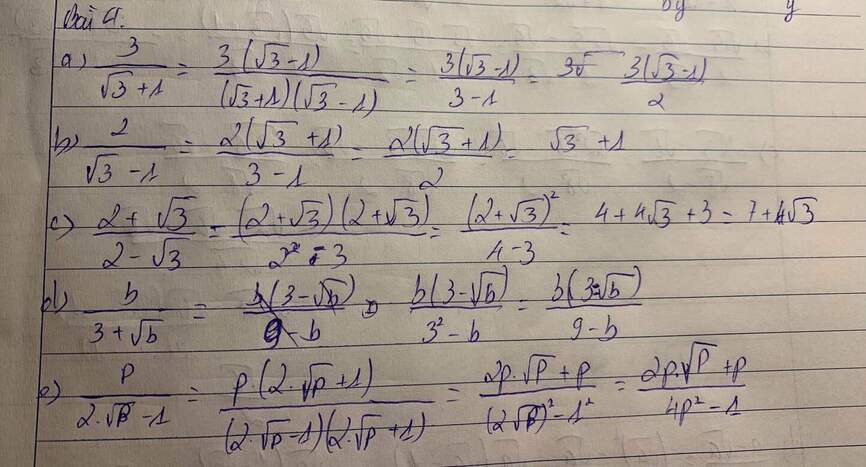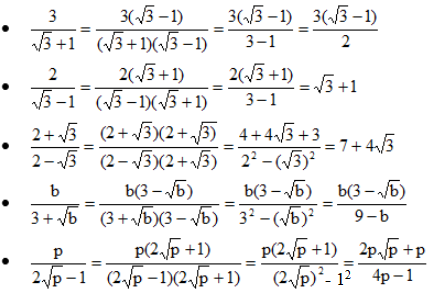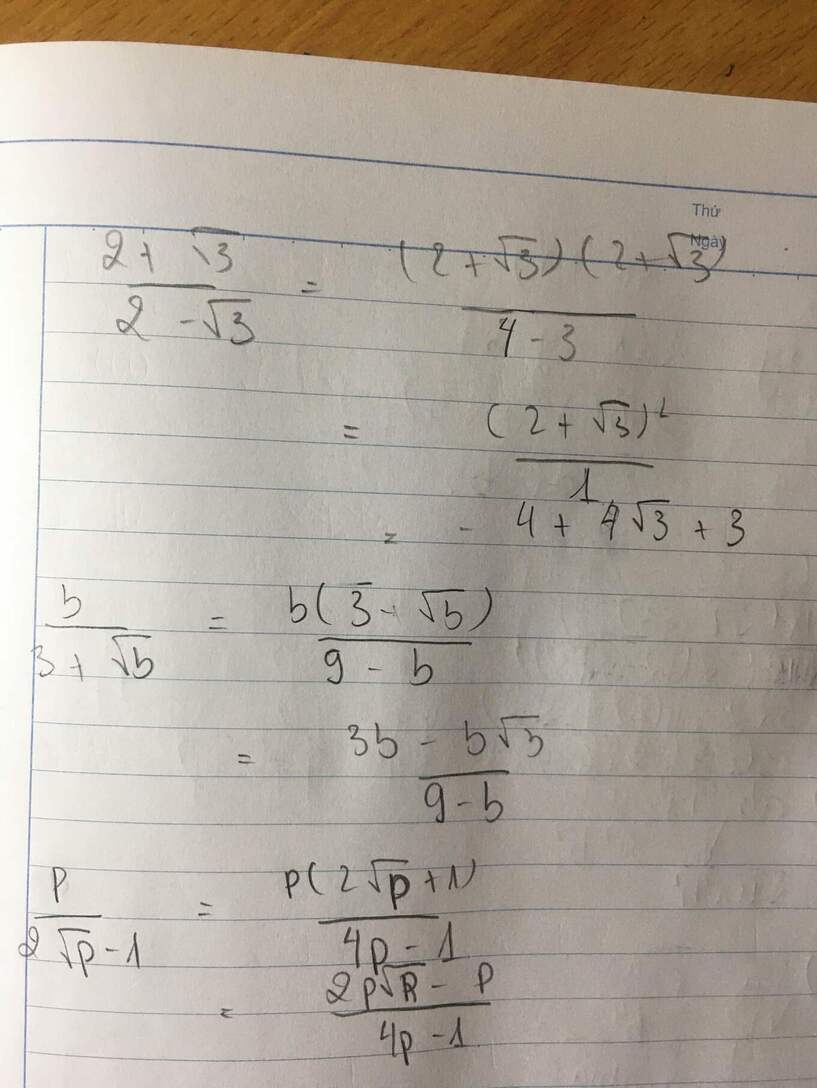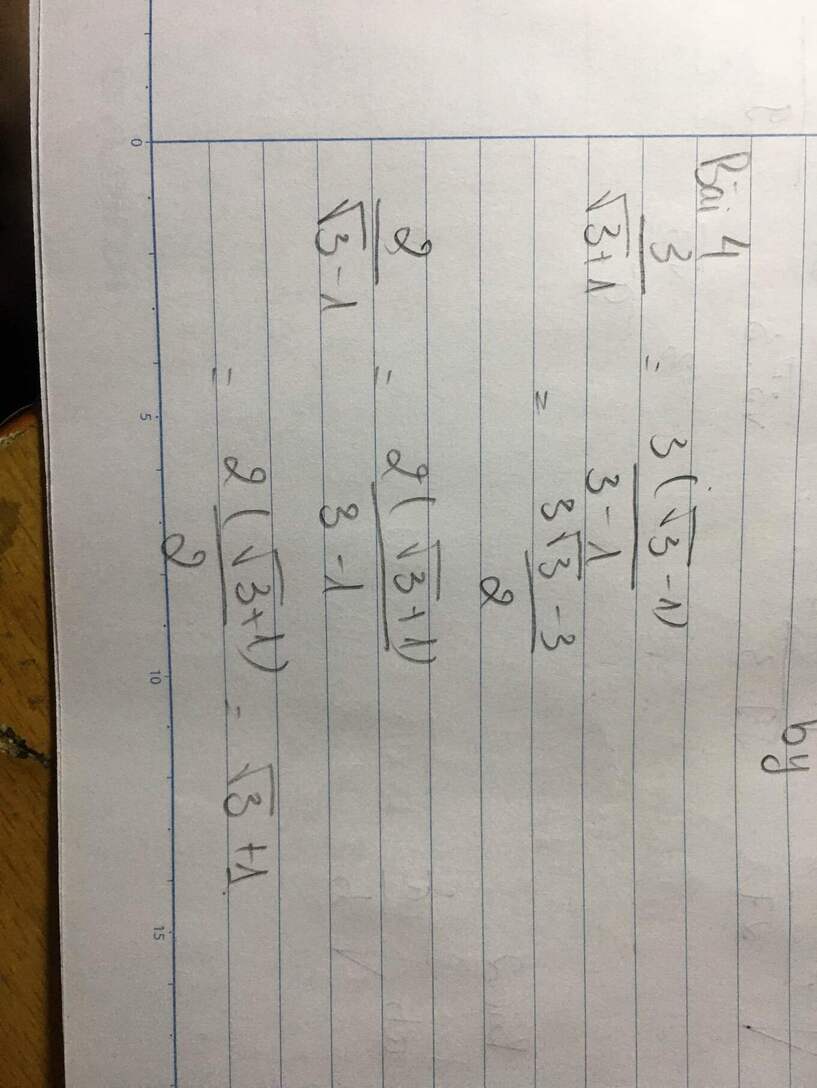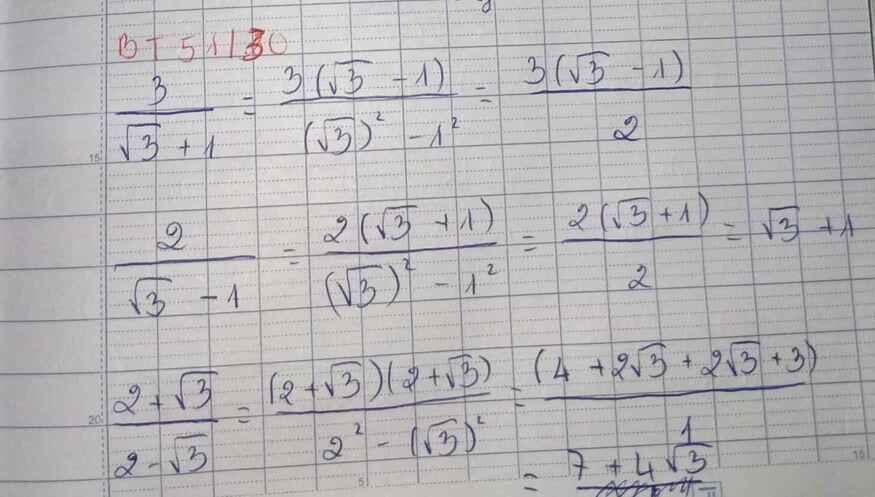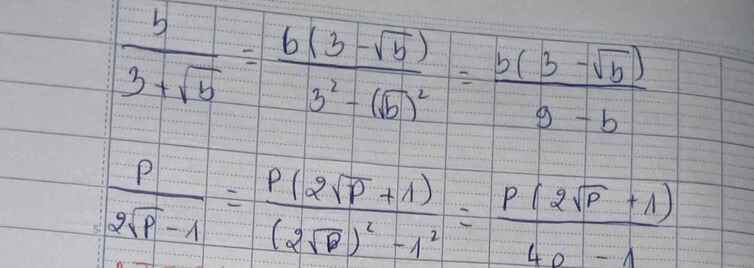Question

Bài 51 (trang 30 SGK Toán 9 Tập 1) 

Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa

$\dfrac{3}{\sqrt{3}+1}$ ; $\dfrac{2}{\sqrt{3}-1}$; $\dfrac{2+\sqrt{3}}{2-\sqrt{3}}$ ;  $\dfrac{b}{3+\sqrt{b}}$ ;  $\dfrac{p}{2 .\sqrt{p}-1}$.

Answer 1

33+1=3(3−1)(3+1)(3−1)=33−3.1(3)2−12" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">33+1=3(3−1)(3+1)(3−1)=33−3.1(3)2−12

33−33−1=33−32" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">33−33−1=33−32.

23−1=2(3+1)(3−1)(3+1)=2(3+1)(3)2−12" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">23−1=2(3+1)(3−1)(3+1)=2(3+1)(3)2−12

2(3+1)3−1=2(3+1)2=3+1" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">2(3+1)3−1=2(3+1)2=3+1.

2+32−3=(2+3).(2+3)(2−3)(2+3)=(2+3)222−(3)2" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">2+32−3=(2+3).(2+3)(2−3)(2+3)=(2+3)222−(3)2

22+2.2.3+(3)24−3" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">22+2.2.3+(3)24−3

7+431=7+43" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">7+431=7+43.

b3+b=b(3−b)(3+b)(3−b)" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">b3+b=b(3−b)(3+b)(3−b)

b(3−b)32−(b)2=b(3−b)9−b;(b≠9)" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">b(3−b)32−(b)2=b(3−b)9−b;(b≠9).

p2p−1=p(2p+1)(2p−1)(2p+1)" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">p2p−1=p(2p+1)(2p−1)(2p+1)

p(2p+1)(2p)2−12=p(2p+1)4p−1" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.36px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">p(2p+1)(2p)2−12=p(2p+1)4p−1

#Ye Chi-Lien

Answer 2

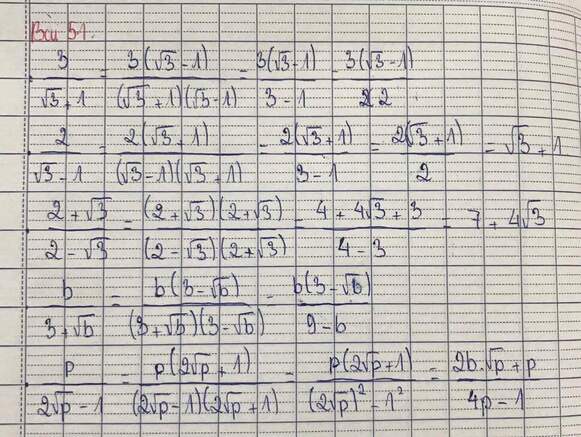
\(\frac{3}{\sqrt{3}+1}=\frac{3\left(\sqrt{3}-1\right)}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}=\frac{3\sqrt{3}-3}{3-1}=\frac{3\sqrt{3}-3}{2}\)

\(\frac{2}{\sqrt{3}-1}=\frac{2\left(\sqrt{3}+1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}=\frac{2\left(\sqrt{3}+1\right)}{3-1}=\sqrt{3}-1\)

\(\frac{2+\sqrt{3}}{2-\sqrt{3}}=\frac{\left(2+\sqrt{3}\right)^2}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)=4-3}=\left(2+\sqrt{3}\right)^2=4+4\sqrt{3}+3=7+4\sqrt{3}\)

\(\frac{b}{3+\sqrt{b}}=\frac{b\left(3-\sqrt{b}\right)}{\left(3+\sqrt{b}\right)\left(3-\sqrt{b}\right)}=\frac{b\left(3-\sqrt{b}\right)}{9-b}\)

\(\frac{p}{2\sqrt{p}-1}=\frac{p\left(2\sqrt{p}+1\right)}{\left(2\sqrt{p}-1\right)\left(2\sqrt{b}+1\right)}=\frac{p\left(2\sqrt{b}+1\right)}{4p-1}\)

Answer 3

+) \dfrac{3}{\sqrt{3}+1}=\dfrac{3(\sqrt{3}-1)}{(\sqrt{3}+1)(\sqrt{3}-1)}=\dfrac{3(\sqrt{3}-1)}{3-1}=\dfrac{3(\sqrt{3}-1)}{2}3​+13​=(3​+1)(3​−1)3(3​−1)​=3−13(3​−1)​=23(3​−1)​.

+) \dfrac{2}{\sqrt{3}-1}=\dfrac{2(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}=\dfrac{2(\sqrt{3}+1)}{3-1}=\sqrt{3}+13​−12​=(3​−1)(3​+1)2(3​+1)​=3−12(3​+1)​=3​+1.

+) \dfrac{2+\sqrt{3}}{2-\sqrt{3}}=\dfrac{(2+\sqrt{3})(2+\sqrt{3)}}{(2-\sqrt{3})(2+\sqrt{3})}=\dfrac{4+4 \sqrt{3}+3}{2^{2}-(\sqrt{3})^{2}}=7+4 \sqrt{3}2−3​2+3​​=(2−3​)(2+3​)(2+3​)(2+3)​​=22−(3​)24+43​+3​=7+43​.

+) \dfrac{b}{3+\sqrt{b}}=\dfrac{b(3-\sqrt{b})}{(3+\sqrt{b})(3-\sqrt{b})}=\dfrac{b(3-\sqrt{b})}{3^{2}-(\sqrt{b})^{2}}=\dfrac{b(3-\sqrt{b})}{9-b}3+b​b​=(3+b​)(3−b​)b(3−b​)​=32−(b​)2b(3−b​)​=9−bb(3−b​)​.

+) \dfrac{p}{2 .\sqrt{p}-1}=\dfrac{p(2 .\sqrt{p}+1)}{(2 .\sqrt{p}-1)(2 .\sqrt{p}+1)}=\dfrac{p(2 \sqrt{p}+1)}{(2 \sqrt{p})^{2}-1^{2}}=\dfrac{2 p.\sqrt{p}+p}{4 p-1}2.p​−1p​=(2.p​−1)(2.p​+1)p(2.p​+1)​=(2p​)2−12p(2p​+1)​=4p−

Answer 4

33+1=3(3−1)(3+1)(3−1)=3(3−1)3−1=3(3−1)2.

23−1=2(3+1)(3−1)(3+1)=2(3+1)3−1=3+1.

2+32−3=(2+3)(2+3)(2−3)(2+3)=4+43+322−(3)2=7+43.

b3+b=b(3−b)(3+b)(3−b)=b(3−b)32−(b)2=b(3−b)9−b.

p2.p−1=p(2.p+1)(2.p−1)(2.p+1)=p(2p+1)(2p)2−12=2p.p+p4p−1.

Answer 5

+) \dfrac{3}{\sqrt{3}+1}=\dfrac{3(\sqrt{3}-1)}{(\sqrt{3}+1)(\sqrt{3}-1)}=\dfrac{3(\sqrt{3}-1)}{3-1}=\dfrac{3(\sqrt{3}-1)}{2}3​+13​=(3​+1)(3​−1)3(3​−1)​=3−13(3​−1)​=23(3​−1)​.

+) \dfrac{2}{\sqrt{3}-1}=\dfrac{2(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}=\dfrac{2(\sqrt{3}+1)}{3-1}=\sqrt{3}+13​−12​=(3​−1)(3​+1)2(3​+1)​=3−12(3​+1)​=3​+1.

+) \dfrac{2+\sqrt{3}}{2-\sqrt{3}}=\dfrac{(2+\sqrt{3})(2+\sqrt{3)}}{(2-\sqrt{3})(2+\sqrt{3})}=\dfrac{4+4 \sqrt{3}+3}{2^{2}-(\sqrt{3})^{2}}=7+4 \sqrt{3}2−3​2+3​​=(2−3​)(2+3​)(2+3​)(2+3)​​=22−(3​)24+43​+3​=7+43​.

+) \dfrac{b}{3+\sqrt{b}}=\dfrac{b(3-\sqrt{b})}{(3+\sqrt{b})(3-\sqrt{b})}=\dfrac{b(3-\sqrt{b})}{3^{2}-(\sqrt{b})^{2}}=\dfrac{b(3-\sqrt{b})}{9-b}3+b​b​=(3+b​)(3−b​)b(3−b​)​=32−(b​)2b(3−b​)​=9−bb(3−b​)​.

+) \dfrac{p}{2 .\sqrt{p}-1}=\dfrac{p(2 .\sqrt{p}+1)}{(2 .\sqrt{p}-1)(2 .\sqrt{p}+1)}=\dfrac{p(2 \sqrt{p}+1)}{(2 \sqrt{p})^{2}-1^{2}}=\dfrac{2 p.\sqrt{p}+p}{4 p-1}2.p​−1p​=(2.p​−1)(2.p​+1)p(2.p​+1)​=(2p​)2−12p(2p​+1)​=4p−12p.p​+p​

Answer 6

\(\dfrac{3}{\sqrt{3}+1}=\dfrac{3(\sqrt{3}-1)}{3-1}=\dfrac{3\sqrt{3}-3}{2}\)

\(\dfrac{2}{\sqrt{3}-1}=\dfrac{2\left(\sqrt{3}+1\right)}{3-1}=\dfrac{2\sqrt{3}+2}{2}=\sqrt{3}+1\)

\(\dfrac{2+\sqrt{3}}{2-\sqrt{3}}=\dfrac{4+4\sqrt{3}+3}{4-3}=4+4\sqrt{3}+3\)

\(\dfrac{b}{3+\sqrt{b}}=\dfrac{b\left(3-\sqrt{b}\right)}{9-b}=\dfrac{3b-b\sqrt{b}}{9-b}\)

\(\dfrac{p}{2\sqrt{p}-1}=\dfrac{p\left(2\sqrt{p}+1\right)}{4p-1}=\dfrac{2p\sqrt{p}+p}{4p-1}\)

Answer 7

\(\dfrac{3}{\sqrt{3}+1}=\dfrac{3\left(\sqrt{3}-1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}=\dfrac{3\left(\sqrt{3}-1\right)}{\left(\sqrt{3}\right)^2-1}=\dfrac{3\left(\sqrt{3}-1\right)}{3-1}\dfrac{3\left(\sqrt{3}-1\right)}{2}\)

\(\dfrac{2}{\sqrt{3}-1}=\dfrac{2\left(\sqrt{3}+1\right)}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}=\dfrac{2\left(\sqrt{3}+1\right)}{\left(\sqrt{3}\right)^2-1}=\dfrac{2\left(\sqrt{3}+1\right)}{3-1}=\sqrt{3}+1\)

\(\dfrac{2+\sqrt{3}}{2-\sqrt{3}}=\dfrac{\left(2+\sqrt{3}\right)\left(2+\sqrt{3}\right)}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}=\dfrac{4+4\sqrt{3}+3}{2^2-\left(\sqrt{3}\right)^2}=\dfrac{7+4\sqrt{3}}{4-3}=7+4\sqrt{3}\)

\(\dfrac{p}{2\sqrt{p}-1}=\dfrac{p\left(2\sqrt{p}+1\right)}{\left(2\sqrt{p}+1\right)\left(2\sqrt{p}-1\right)}=\dfrac{2p\sqrt{p}+p}{\left(2p\right)^2-1}=\dfrac{2p\sqrt{p}+p}{4p-1}\)

\(\dfrac{b}{3+\sqrt{b}}=\dfrac{b\left(3-\sqrt{b}\right)}{\left(3+\sqrt{b}\right)\left(3-\sqrt{b}\right)}=\dfrac{b\left(3-\sqrt{b}\right)}{3^2-\left(\sqrt{b}\right)^2}=\dfrac{b\left(3-\sqrt{b}\right)}{9-b}\)

Answer 8

Answer 9

\(\dfrac{3\sqrt{3}-3}{2}\);\(\dfrac{2\sqrt{3}+2}{2}\);\(7+4\sqrt{3}\);\(\dfrac{b\sqrt{b}-3b}{b-9}\);\(\dfrac{2p\sqrt{p}+p}{4p-1}\)

Answer 10

 

Answer 11

Answer 12

+) \dfrac{3}{\sqrt{3}+1}=\dfrac{3(\sqrt{3}-1)}{(\sqrt{3}+1)(\sqrt{3}-1)}=\dfrac{3(\sqrt{3}-1)}{3-1}=\dfrac{3(\sqrt{3}-1)}{2}3​+13​=(3​+1)(3​−1)3(3​−1)​=3−13(3​−1)​=23(3​−1)​.

+) \dfrac{2}{\sqrt{3}-1}=\dfrac{2(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}=\dfrac{2(\sqrt{3}+1)}{3-1}=\sqrt{3}+13​−12​=(3​−1)(3​+1)2(3​+1)​=3−12(3​+1)​=3​+1.

+) \dfrac{2+\sqrt{3}}{2-\sqrt{3}}=\dfrac{(2+\sqrt{3})(2+\sqrt{3)}}{(2-\sqrt{3})(2+\sqrt{3})}=\dfrac{4+4 \sqrt{3}+3}{2^{2}-(\sqrt{3})^{2}}=7+4 \sqrt{3}2−3​2+3​​=(2−3​)(2+3​)(2+3​)(2+3)​​=22−(3​)24+43​+3​=7+43​.

+) \dfrac{b}{3+\sqrt{b}}=\dfrac{b(3-\sqrt{b})}{(3+\sqrt{b})(3-\sqrt{b})}=\dfrac{b(3-\sqrt{b})}{3^{2}-(\sqrt{b})^{2}}=\dfrac{b(3-\sqrt{b})}{9-b}3+b​b​=(3+b​)(3−b​)b(3−b​)​=32−(b​)2b(3−b​)​=9−bb(3−b​)​.

+) \dfrac{p}{2 .\sqrt{p}-1}=\dfrac{p(2 .\sqrt{p}+1)}{(2 .\sqrt{p}-1)(2 .\sqrt{p}+1)}=\dfrac{p(2 \sqrt{p}+1)}{(2 \sqrt{p})^{2}-1^{2}}=\dfrac{2 p.\sqrt{p}+p}{4 p-1}2.p​−1p​=(2.p​−1)(2.p​+1)p(2.p​+1)​=(2p​)2−12p(2p​+1)​=4p−12p.p​+p​.

Answer 13

Answer 14

Answer 15

33+1=3(3−1)(3+1)(3−1)=3(3−1)3−1=3(3−1)2.

 

23−1=2(3+1)(3−1)(3+1)=2(3+1)3−1=3+1.

 

2+32−3=(2+3)(2+3)(2−3)(2+3)=4+43+322−(3)2=7+43.

 

b3+b=b(3−b)(3+b)(3−b)=b(3−b)32−(b)2=b(3−b)9−b.

 

p2.p−1=p(2.p+1)(2.p−1)(2.p+1)=p(2p+1)(2p)2−12=2p.p+p4p−1.

Answer 16

Answer 17

+) \dfrac{3}{\sqrt{3}+1}=\dfrac{3(\sqrt{3}-1)}{(\sqrt{3}+1)(\sqrt{3}-1)}=\dfrac{3(\sqrt{3}-1)}{3-1}=\dfrac{3(\sqrt{3}-1)}{2}3​+13​=(3​+1)(3​−1)3(3​−1)​=3−13(3​−1)​=23(3​−1)​.

+) \dfrac{2}{\sqrt{3}-1}=\dfrac{2(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}=\dfrac{2(\sqrt{3}+1)}{3-1}=\sqrt{3}+13​−12​=(3​−1)(3​+1)2(3​+1)​=3−12(3​+1)​=3​+1.

+) \dfrac{2+\sqrt{3}}{2-\sqrt{3}}=\dfrac{(2+\sqrt{3})(2+\sqrt{3)}}{(2-\sqrt{3})(2+\sqrt{3})}=\dfrac{4+4 \sqrt{3}+3}{2^{2}-(\sqrt{3})^{2}}=7+4 \sqrt{3}2−3​2+3​​=(2−3​)(2+3​)(2+3​)(2+3)​​=22−(3​)24+43​+3​=7+43​.

+) \dfrac{b}{3+\sqrt{b}}=\dfrac{b(3-\sqrt{b})}{(3+\sqrt{b})(3-\sqrt{b})}=\dfrac{b(3-\sqrt{b})}{3^{2}-(\sqrt{b})^{2}}=\dfrac{b(3-\sqrt{b})}{9-b}3+b​b​=(3+b​)(3−b​)b(3−b​)​=32−(b​)2b(3−b​)​=9−bb(3−b​)​.

+) \dfrac{p}{2 .\sqrt{p}-1}=\dfrac{p(2 .\sqrt{p}+1)}{(2 .\sqrt{p}-1)(2 .\sqrt{p}+1)}=\dfrac{p(2 \sqrt{p}+1)}{(2 \sqrt{p})^{2}-1^{2}}=\dfrac{2 p.\sqrt{p}+p}{4 p-1}2.p​−1p​=(2.p​−1)(2.p​+1)p(2.p​+1)​=(2p​)2−12p(2p​+1)​=4p−12p.p​+p​.

Answer 18

Answer 19

a\(\dfrac{3\left(\sqrt{3}-1\right)}{2}\)b\(\sqrt{3}+1\)c7+\(4\sqrt{3}\)d\(\dfrac{3b-b\sqrt{b}}{3-b}\)e\(\dfrac{p\left(\sqrt{p}+1\right)}{2\left(p-1\right)}\)

Answer 20

+) 3√3+1=3(√3−1)(√3+1)(√3−1)=3(√3−1)3−1=3(√3−1)2.

+) 2√3−1=2(√3+1)(√3−1)(√3+1)=2(√3+1)3−1=√3+1.

2=7+4√3.

2=b(3−√b)9−b.

2=2p.√p+p4p−1

Answer 21

Answer 22

Answer 23

2p.canp+p/4p-1

Answer 24

 

 

Answer 25

Answer 26

 

 

Answer 27

 

Answer 28

Answer 29

 

Answer 30