Bài 5: Cho tam giác ABC, trung tuyến AM. Từ M kẻ đường thẳng song song với AB cắt AC tại N. Biết ANMN; BN cắt AM ở O. Chứng minh:a) Tam giác ABC cân ở Ab) O là trọng tâm của tam giác ABCBài 6: Cho tam giác ABC vuông tại A, phân giác CD. Gọi H là hình chiếu của điểm B trên đường thẳng CD. Trên CD lấy điểm E sao cho H là trung điểm của DE. Gọi F là giao điểm của BH và CA. Chứng minh:a) Góc CEB góc ADC và Góc EBH góc ACDb) BE vuông góc BCC) DF song song BEBài 7: Cho tam giác ABC vuông tại A, có AC1...
Đọc tiếp
Bài 5: Cho tam giác ABC, trung tuyến AM. Từ M kẻ đường thẳng song song với AB cắt AC tại N. Biết AN=MN; BN cắt AM ở O. Chứng minh:
a) Tam giác ABC cân ở A
b) O là trọng tâm của tam giác ABC
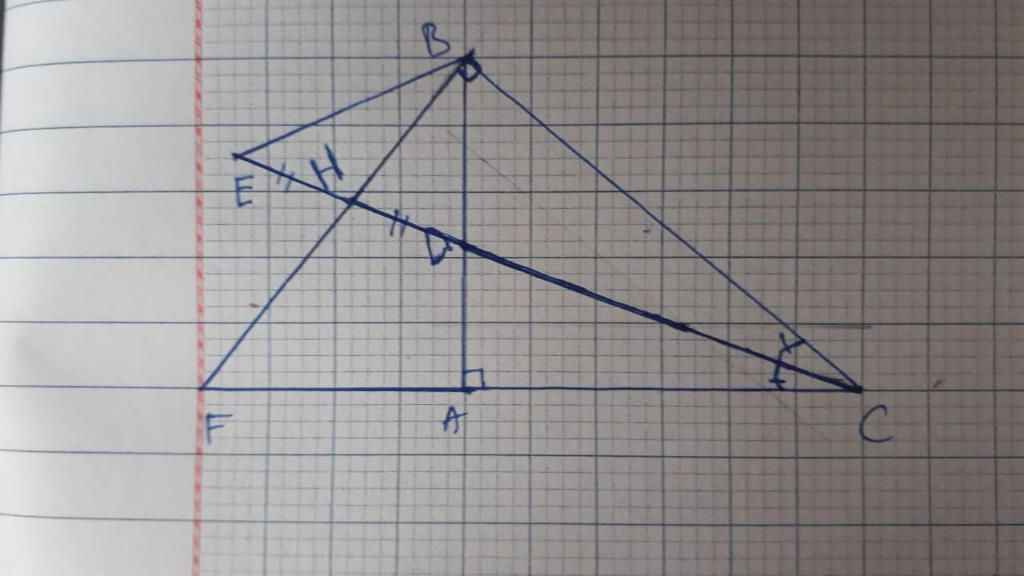
Bài 6: Cho tam giác ABC vuông tại A, phân giác CD. Gọi H là hình chiếu của điểm B trên đường thẳng CD. Trên CD lấy điểm E sao cho H là trung điểm của DE. Gọi F là giao điểm của BH và CA. Chứng minh:
a) Góc CEB= góc ADC và Góc EBH= góc ACD
b) BE vuông góc BC
C) DF song song BE
Bài 7: Cho tam giác ABC vuông tại A, có AC=12cm, BC-13cm. Gọi I là trung điểm của BC. Trên tia AI lấy điểm K sao cho IA=IK
a) Tính AB
b)Chứng minh rằng: Tam giác IAB= tam giác IKC, từ đó suy ra tam giác ACK là tam giác vuông
c) Gọi điểm M là trung điểm của AC.Chứng minh: MB=MK
d) MK cắt BC tại N,BM cắt AI tại E. Chứng minh: tam giác MEN cân;EN song song BK
Bài 8: Cho tam giác ABC vuông tại A, có AB= 8cm, BC= 17cm
a) Tính AC
b) Trung trực của BC cắt AC tại D và cắt AB tại F. Chứng minh: Góc DBC= góc DCB
c) Trên tia đối của tia DB lấy điểm E sao cho DE=DC. Chứng minh tam giác BEC vuông. Suy ra DF là phân giác của góc ADE
d) Chứng minh: BE vuông góc với FC