Các câu hỏi tương tự
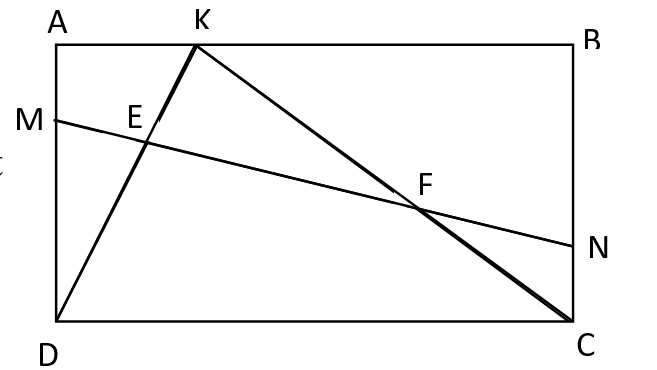
Cho hình chữ nhật ABCD có AMNC,K bất kỳ, MN cắt KD và KC lần lượt tại E,F. So sánh diện tích tam giác KEF với tổng diện tích hai tam giác MDE và CNF.
Đọc tiếp
Cho hình chữ nhật ABCD có AM=NC,K bất kỳ, MN cắt KD và KC lần lượt tại E,F. So sánh diện tích tam giác KEF với tổng diện tích hai tam giác MDE và CNF.
Cho hình vuông ABCD.D,E lần lượt là trung điểm chính giữa của AB và AC,AD cắt BE tại I
a]So sánh IAE và IBC
b]Chứng tỏ 3 tam giác ABI,BCI,CAI bằng nhau
Bài 1 cho tứ giác ABCD, P,Q lần lượt là trung điểm của AD và BC,a chứng minh PQ hoặc AB AC 2,b tứ giác ABCD là hình thang PQ AB CD 2. Bài 2 cho hình thang ABCD, AB đáy lớn. M ,N,P,Q lần lượt là trung điểm của AD BC AC BD.a chứng Minh M N P Q thẳng hàng.b Cho AB a CD b với a b. Tính MN PQ.c Cm rằng nếu MP PQ QN thì a 2b
Hình chữ nhật ABCD có 5 lần chiều dài =8 lần chiều rộng và có chu vi là 52 m . Trên các cạnh AB,BC,CD,DA lần lượt lấy các điểm chính giữa M,N,P,Q. Tính diện tích MNPQ ?
P/s: Giúp mình vs, ai đúng và nhanh mình tick cho !
Hình chữ nhật ABCD có 5 lần chiều dài =8 lần chiều rộng và có chu vi là 52 m . Trên các cạnh AB,BC,CD,DA lần lượt lấy các điểm chính giữa M,N,P,Q. Tính diện tích MNPQ ?
P/s: Giúp mình vs, ai đúng và nhanh mình tick cho !
Hình chữ nhật ABCD có 5 lần chiều dài =8 lần chiều rộng và có chu vi là 52 m . Trên các cạnh AB,BC,CD,DA lần lượt lấy các điểm chính giữa M,N,P,Q. Tính diện tích MNPQ ?
P/s: Giúp mình vs, ai đúng và nhanh mình tick cho
Cho hình chữ nhật ABCD có cạnh AB = 12cm, cạnh AD = 6cm. Lấy trên cạnh AD lấy điểm P, trên cạnh BC điểm Q sao cho AP=CQ
a)Tính diện tích hình thang ABQP và diện tích hình thang DPQC.
b)Trên cạnh AB lấy điểm M. Nối MD và MC cắt PQ lần lượt tại E, F. Hãy chứng tỏ rằng diện tích hình tam giác MEF bằng tổng diện tích hai hình tam giác DEP và CFQ
trên cạnh AB của hình tam giác ABC lấy hai điểm D,E sao cho ADDEEB trên cạnh BC lấy hai điểm M và N sao cho BMMNNC trên cạnh AC lấy 2 điểm P và Q sao cho CPPQQA tia AM cắt các đoạn thẳng DQ và EP lần lượt tại U V tia AN cắt các đoạn thẳng DQ và EP lần lượt tại X,Ya) so sanh do dai cac doan thang AU,UV,VMb) so sánh diện tích hình tứ giác XVYX voi diện tích hình tam giác ABCLÀM CẢ BÀI GIẢI RA CHO MÌNH NHÉ :))
Đọc tiếp
trên cạnh AB của hình tam giác ABC lấy hai điểm D,E sao cho AD=DE=EB trên cạnh BC lấy hai điểm 'M và N sao cho BM=MN=NC trên cạnh AC lấy 2 điểm P và Q sao cho CP=PQ=QA tia AM cắt các đoạn thẳng DQ và EP lần lượt tại U V tia AN cắt các đoạn thẳng DQ và EP lần lượt tại X,Y
a) so sanh do dai cac doan thang AU,UV,VM
b) so sánh diện tích hình tứ giác XVYX voi diện tích hình tam giác ABC
LÀM CẢ BÀI GIẢI RA CHO MÌNH NHÉ :))
cho tam giác ABC có .D,E lần lượt là các điểm chính giữa cạnh AC và AB .2 đoạn thẳng BD và CE cắt tại G . kéo dài AG cắt BC tại M
a) MB so với MC
b )so sánh AG với AM
c) chứng minh ED song song với BC