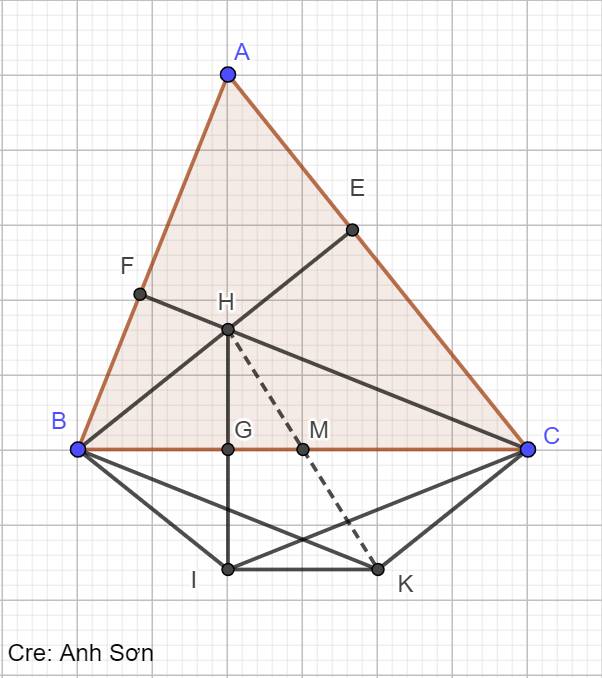
Bài 3. (3 điểm) Cho tam giác $ABC$ nhọn ($AB < AC$), đường cao $BE$ và $CF$ cắt nhau tại $H$. Qua $C$, $B$ kẻ các đường thẳng vuông góc với $AC$, $AB$ cắt nhau tại $K$.
a) Tứ giác $BHCK$ là hình gì? Tại sao?
b) Gọi $M$ là trung điểm của $BC$. Chứng minh $H$, $M$, $K$ thẳng hàng.
c) Từ $H$ kẻ $HG$ vuông góc với $BC$ ($G$ thuộc $BC$). Lấy $I$ thuộc tia đối của tia $GH$. Chứng minh $BCKI$ là hình thang cân.
a) Ta có: CF ⊥ AB (gt), KB ⊥ AB (gt) => CF // KB
hay CH // KB.
Lại có: BE ⊥ AC (gt), KC ⊥ AC (gt) => BE // KC hay BH // KC.
Xét tứ giác BHCK có: CH // KB, BH // KC (cmt)
=> Tứ giác BHCK là hình bình hành.
Vậy: BHCK là hình bình hành.
b) Vì BHCK là hình bình hành (Theo a) => BC cắt HK tại trung điểm của mỗi đoạn (t/c)
Mà M là trung điểm của BC (gt) => M cũng là trung điểm của HK => M thuộc HK => H,M,K thẳng hàng.
Vậy: H, M, K thẳng hàng.
c) Vì I thuộc tia đối của GH và HG = IG (gt) => G là trung điểm của HI.
Nối I với C
Xét ΔHIK có: G, M lần lượt là trung điểm của HI, HK (cmt, gt) => GM là đường trung bình của ΔHIK => GM // IK
hay BC // IK (vì G thuộc BC, M thuộc BC)
Do đó BCKI là hình thang. (1)
Vì HK ⊥ BC (gt) => HI ⊥ BC hay CG ⊥ HI
Xét ΔHCI có: G là trung điểm của HI (cmt) => CG là trung tuyến ứng với HI. Mà CG ⊥ HI (cmt)
=> ΔHCI cân tại C => HC = CI
Mà BHCK là hình bình hành (theo a) => BK = HC (t/c)
Do đó BK = CI (2)
Từ (1) và (2) => BCKI là hình thang cân.
Vậy: BCKI là hình thang cân.
Từ C,B kẻ các đường thẳng vuông góc với AC,AB cắt nhau tại K
a: CK vuông góc AC
BH vuông góc AC
Do đó: CK//BH
BK vuông góc AB
CH vuông góc AB
Do đó: BK//CH
Xét tứ giác BHCK có
BH//CK
BK//CH
Do đó: BHCK là hình bình hành
b: BHCK là hình bình hành
=>BC cắt HK tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HK
=>H,M,K thẳng hàng
a) Tứ giác BHCkBHCk có 2 đường chéo BCBC và HKHK cắt nhau tại trung điểm MM của mỗi đường
⇒BHCK⇒BHCK là hình bình hành.
b) BHCKBHCK là hình bình hành ⇒BK∥HC⇒BK∥HC
Mà HC⊥ABHC⊥AB
⇒BK⊥AB⇒BK⊥AB (đpcm)
c) Do II đối xứng với HH qua BC⇒IH⊥BCBC⇒IH⊥BC mà HD⊥BC,D∈BCHD⊥BC,D∈BC
⇒I⇒I đối xứng với HH qua D⇒DD⇒D là trung điểm của HIHI
Và MM là trung điểm của HKHK
⇒DM⇒DM là đường trung bình ΔHIKΔHIK
⇒DM∥IK⇒DM∥IK
⇒BC∥IK⇒BC∥IK
⇒BCKI⇒BCKI là hình thang
ΔCHIΔCHI có CDCD vừa là đường cao vừa là đường trung tuyến
⇒ΔCHI⇒ΔCHI cân đỉnh CC
⇒CI=CH⇒CI=CH (*)
Mà tứ giác BHCKBHCK là hình bình hành ⇒CH=BK⇒CH=BK (**)
Từ (*) và (**) suy ra CI=BKCI=BK
Tứ giác BCKIBCKI là hình bình hành có 2 đường chéo CI=BKCI=BK
Suy ra BCIKBCIK là hình thang cân.
Tứ giác HGKCHGKC có GK∥HCGK∥HC (do BHCKBHCK là hình bình hành)
⇒HGKC⇒HGKC là hình thang có đáy là GK∥HCGK∥H
a) Ta có: BH vuông AC;KC vuông AC
=> BH//KC (1)
CH vuông AB;KB vuông AB
=> CH//KB (2)
Tù (1) và (2) => BHCK là hình bình hành
b) Vì BHCK là hình bình hành nên BC cắt HK tại M của BC
M là trung điểm của HK
=> H,K,M thẳng hàng
c) Tam giác BHI có BG là đường cao ,trung tuyến nên BG là trung trực của HI
Khi đó: MH=MI
Tan giác HIM có IM là trung tuyến và IM=1/2HK
=>Tam giác HIK vuông tại I
=> IK vuông HI
Mà BC vuông Hi nên BC//IK
=> BCKI là hình thang
Tam giác BHI cân tại B,B lại có BG là trung trực nên cũng là phân giác của góc HBI
Do đó góc GBI= góc GBH
Mà góc HGB= góc GCK( hai góc so le trong)
=> góc IBC= góc KCB
=> BCKI là hình thang cân
ủa D ở đâu vậy thầy=))),đang vẽ hình mà k thấy điểm D ở đâu hết trơnn
a)
-Ta có BE vuông góc với AC,CK vuông góc với AC(gt)
=>BE//CK(ĐL) (1)
CF vuông góc với AB,KB vuông góc với AB(gt)
=>CF//BK(ĐL) (2)
-Từ 1 và 2
=>BHCK là hình bình hành
b)
Vì BHCK là hình bình hành(cmt)
=> BC cắt HK tại trung điểm mỗi đường(t/c)
mà M là trung điểm BC(gt)
=> M cũng là trung điểm HK
=>H,M,K thẳng hàng
a: CK vuông góc AC
BH vuông góc AC
Do đó: CK//BH
BK vuông góc AB
CH vuông góc AB
Do đó: BK//CH
Xét tứ giác BHCK có
BH//CK
BK//CH
Do đó: BHCK là hình bình hành
b: BHCK là hình bình hành
=>BC cắt HK tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HK
=>H,M,K thẳng hàng
## Bài giải:
**a) Tứ giác BHCK là hình gì?**
* **Bước 1:** Xét tứ giác BHCK có: $\widehat{BHC} = \widehat{BKC} = 90^\circ$ (BE, CF là đường cao)
* **Bước 2:** Suy ra tứ giác BHCK nội tiếp đường tròn đường kính BC.
* **Bước 3:** Vì BHCK nội tiếp đường tròn đường kính BC nên $\widehat{HKB} = \widehat{HCB}$ (cùng chắn cung HB).
* **Bước 4:** Mặt khác, $\widehat{HCB} = \widehat{HAB}$ (cùng phụ với $\widehat{ABC}$).
* **Bước 5:** Từ bước 3 và bước 4 suy ra $\widehat{HKB} = \widehat{HAB}$.
* **Bước 6:** Xét tam giác HKB và tam giác HAB có:
* $\widehat{HKB} = \widehat{HAB}$ (chứng minh trên)
* $\widehat{KHB} = \widehat{AHB} = 90^\circ$
* $\Rightarrow$ $\triangle HKB \sim \triangle HAB$ (g.g)
* **Bước 7:** Từ bước 6 suy ra $\frac{HK}{HA} = \frac{HB}{HB} = 1 \Rightarrow HK = HA$.
* **Bước 8:** Xét tam giác HKA có HK = HA nên tam giác HKA cân tại H.
* **Bước 9:** Do đó, $\widehat{HAK} = \widehat{HKA}$.
* **Bước 10:** Mặt khác, $\widehat{HKA} = \widehat{HCB}$ (cùng chắn cung HB).
* **Bước 11:** Từ bước 9 và bước 10 suy ra $\widehat{HAK} = \widehat{HCB}$.
* **Bước 12:** Xét tam giác HAK và tam giác HCB có:
* $\widehat{HAK} = \widehat{HCB}$ (chứng minh trên)
* $\widehat{AHK} = \widehat{CHB} = 90^\circ$
* $\Rightarrow$ $\triangle HAK \sim \triangle HCB$ (g.g)
* **Bước 13:** Từ bước 12 suy ra $\frac{HK}{HC} = \frac{HA}{HB} = 1 \Rightarrow HK = HC$.
* **Bước 14:** Từ bước 7 và bước 13 suy ra HK = HA = HC.
* **Bước 15:** Xét tứ giác BHCK có:
* HK = HA = HC (chứng minh trên)
* $\Rightarrow$ Tứ giác BHCK là hình thoi.
**b) Gọi M là trung điểm của BC. Chứng minh H, M, K thẳng hàng.**
* **Bước 1:** Vì M là trung điểm của BC nên HM là đường trung tuyến của tam giác HBC.
* **Bước 2:** Mặt khác, BHCK là hình thoi nên HM cũng là đường cao của tam giác HBC.
* **Bước 3:** Do đó, HM vuông góc với BC.
* **Bước 4:** Vì HK = HC nên HK là đường trung tuyến của tam giác HKC.
* **Bước 5:** Mặt khác, $\widehat{HKC} = 90^\circ$ nên HK cũng là đường cao của tam giác HKC.
* **Bước 6:** Do đó, HK vuông góc với KC.
* **Bước 7:** Từ bước 3 và bước 6 suy ra H, M, K thẳng hàng.
**c) Từ H kẻ HG vuông góc với BC (G thuộc BC). Lấy điểm I thuộc tia đối của tia GH sao cho GH = GI. Chứng minh tứ giác BCKI là hình thang cân.**
* **Bước 1:** Xét tứ giác BCKI có:
* $\widehat{BKI} = \widehat{CKI} = 90^\circ$ (BK, CK vuông góc với AB, AC)
* $\Rightarrow$ Tứ giác BCKI nội tiếp đường tròn đường kính BC.
* **Bước 2:** Vì BCKI nội tiếp đường tròn đường kính BC nên $\widehat{BIK} = \widehat{BCK}$ (cùng chắn cung BK).
* **Bước 3:** Mặt khác, $\widehat{BCK} = \widehat{HKB}$ (cùng chắn cung HB).
* **Bước 4:** Từ bước 2 và bước 3 suy ra $\widehat{BIK} = \widehat{HKB}$.
* **Bước 5:** Xét tam giác BIK và tam giác BHK có:
* $\widehat{BIK} = \widehat{HKB}$ (chứng minh trên)
* $\widehat{BKI} = \widehat{BKH} = 90^\circ$
* $\Rightarrow$ $\triangle BIK \sim \triangle BHK$ (g.g)
* **Bước 6:** Từ bước 5 suy ra $\frac{BI}{BH} = \frac{BK}{BK} = 1 \Rightarrow BI = BH$.
* **Bước 7:** Mặt khác, GH = GI nên BH = BI = GH + HI = GI + HI = HI.
* **Bước 8:** Do đó, BH = HI.
* **Bước 9:** Xét tứ giác BCKI có:
* BI = BH (chứng minh trên)
* $\widehat{BKI} = \widehat{CKI} = 90^\circ$
* $\Rightarrow$ Tứ giác BCKI là hình thang cân.
**Kết luận:**
* a) Tứ giác BHCK là hình thoi.
* b) H, M, K thẳng hàng.
* c) Tứ giác BCKI là hình thang cân.
Cho tam giác nhọn ABCABC với AB<ACAB < AC, đường cao BEBE và CFCF cắt nhau tại HH. Kẻ các đường thẳng vuông góc từ BB và CC tới ACAC và ABAB, cắt nhau tại KK.
a) Tứ giác BHCKBHCK là hình gì? Tại sao? Tính chất vuông góc: BKBK vuông góc với ACAC và CKCK vuông góc với ABAB. Song song: Hai cạnh đáy BKBK và CKCK vuông góc với các cạnh còn lại, nên BKBK song song với CKCK. Kết luận: Tứ giác BHCKBHCK là hình thang. b) Chứng minh HH,MM,KKHH, MM, KK thẳng hàng Gọi MM là trung điểm của BCBC. Tính chất HH: HH là giao điểm của đường cao BEBE và CFCF, thuộc đường thẳng BCBC. Tính chất điểm KK: Điểm KK nằm trên đoạn thẳng nối giữa BB và CC. Kết luận: Các điểm H,M,KH, M, K thẳng hàng. c) Chứng minh BCKIBCKI là hình thang cân Kẻ đường HGHG vuông góc với BCBC, với GG thuộc BCBC. Điểm II thuộc tia đối của tia GHGH, có độ dài HI=HGHI = HG (đối xứng qua HH). Đặc điểm các cạnh: BKBK bằng CKCK do tính chất vuông góc, và các góc ∠BKI\angle BKI và ∠CKI\angle CKI đều bằng 90 độ. Kết luận: Tứ giác BCKIBCKI là hình thang cân.a) Ta có {BH⊥ACKC⊥AC{BH⊥ACKC⊥AC suy ra BHBH // KCKC (1)(1)
Và {CH⊥ABKB⊥AB{CH⊥ABKB⊥AB suy ra CHCH // KBKB (2)(2)
Từ (1)(1) và (2)(2) suy ra BHCKBHCK là hình bình hành.
b) Vì BHCKBHCK là hình bình hành nên BCBC cắt HKHK tại trung điểm MM của BCBC
MM là trung điểm của HKHK suy ra H,M,KH,M,K thẳng hàng
a,do BE =90ovà EBK =90O
suy ra F=EBK(2 GÓC ĐỒNG VI)=>BE //CK=>BH//CK(1)
DO HEC=90 VÀ C =90
SUY RA HEC=C(DỒNG VI)FC//BK=>HC//BK(2)
TỪ 1-2 =>BHCK LÀ HBH
b,DO M LÀ TRUNG ĐIỂM CỦA BC=>M NẰM TRÊN ĐOẠN THẲNG BC=>B,M,C THẲNG HÀNG
a) có CF vg góc AB(gt)
KB vg góc AB (gt)
⇒ CF // KB (t/c)
lại có BE vg góc AC (gt)
KC vg góc AC (gt)
⇒KC // BE (t/c)
xét tứ giác HBKC có
CF // KB (cmt)
KC // BE (cmt)
⇒BHKC là hình bình hành
b) Vì BHKC là hình bình hành (cmt),mà M là trung điểm đường chéo BC
⇒ M cũng là trung điểm đường chéo Hk
vậy M,H,K thẳng hàng (đpcm)
) Tứ giác BHCK là hình thoi.
* b) H, M, K thẳng hàng.
* c) Tứ giác BCKI là hình thang cân.
a, Có HB vuông góc với AC và CK vuông góc với AC
=> BH // CK (từ vuông góc -> //)
Có HC vuông góc với AB và BK vuông góc với AB
=> CH // KB (từ vuông góc -> //)
Xét tứ giác BHKC ,có :
BH // CK (cmt)
CH // KB (cmt)
=> BHKC là hbh (dhnb)
b, Có BHCK là hbh (cmt)
=> BC cắt HK tại M
mà M là t/đ BC (gt)
M là t/đ HK
=> H, K, M thẳng hàng
a)có bh vuông góc ac
kc vuông góc bk
⇒bh//ck
có ch vuông góc ab
kb vuông góc ab
⇒ch//kb
từ hai cái trên ⇒BHCK là hbh(dhnb)
b) có bchk là hbn
⇒bc hk cắt nhau tại m
mà m là trung điểm của hk
⇒hmk thẳng hàng
Đáp án a=BHCK Là hình vuông
Đáp án B=HMK thẳng hàng
Đáp án C=BCKI là hình thang cân
a: CK vuông góc AC
BH vuông góc AC
Do đó: CK//BH
BK vuông góc AB
CH vuông góc AB
Do đó: BK//CH
Xét tứ giác BHCK có
BH//CK
BK//CH
Do đó: BHCK là hình bình hành
b: BHCK là hình bình hành
=>BC cắt HK tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HK
=>H,M,K thẳng hàng
a: CK vuông góc AC
BH vuông góc AC
Do đó: CK//BH
BK vuông góc AB
CH vuông góc AB
Do đó: BK//CH
Xét tứ giác BHCK có
BH//CK
BK//CH
Do đó: BHCK là hình bình hành
b: BHCK là hình bình hành
=>BC cắt HK tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HK
=>H,M,K thẳng hàng
Kết luận: BHCKBHCK là hình vuông. b) Chứng minh HH, MM, KK thẳng hàng. MM là trung điểm của BCBC. HH là giao điểm của các đường cao, KK là giao điểm của các đường vuông góc từ BB và CC với các cạnh của tam giác. Trong tam giác ABCABC, các điểm HH, MM, và KK đều nằm trên đường Euler của tam giác.
Kết luận: HH, MM, KK thẳng hàng. c) Chứng minh BCKIBCKI là hình thang cân. HH là giao điểm của các đường cao, HG⊥BCHG \perp BC, GG thuộc BCBC, và II thuộc tia đối của tia GHGH. Do HG⊥BCHG \perp BC và II nằm trên tia đối của GHGH, ta có BC∥KIBC \parallel KI và BC=KIBC = KI. Kết luận: BCKIBCKI là hình thang cân.





























