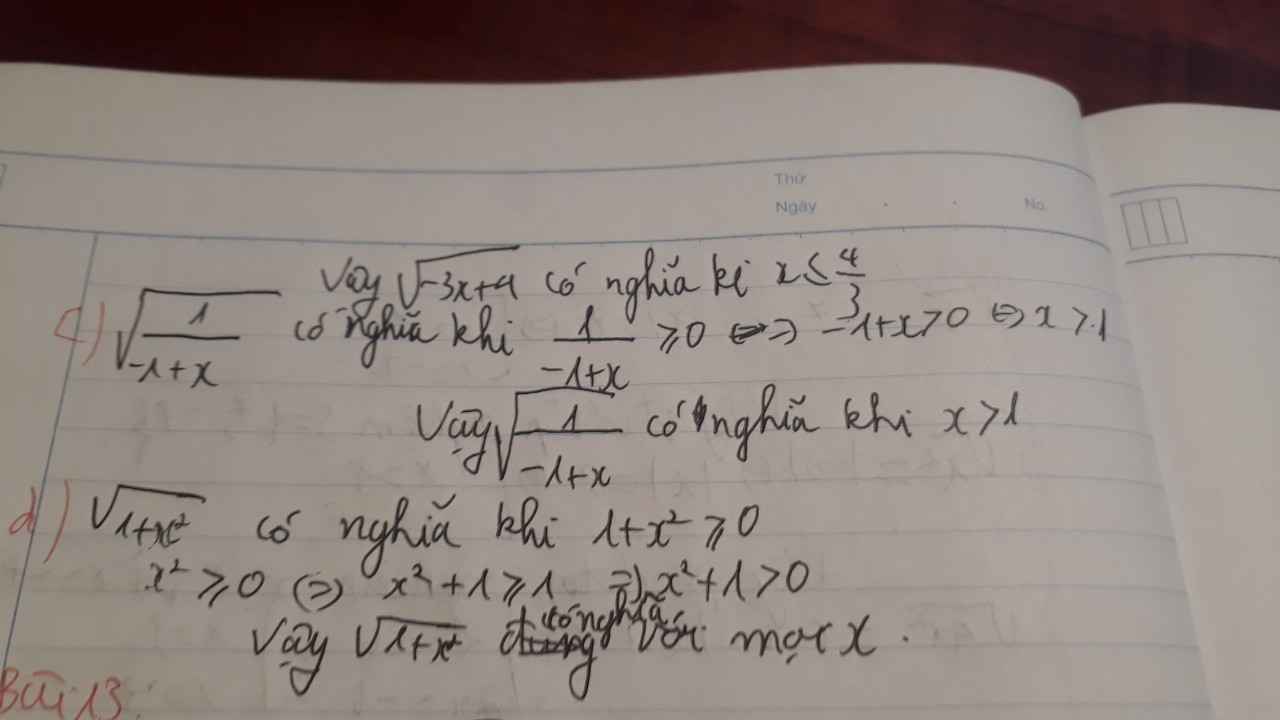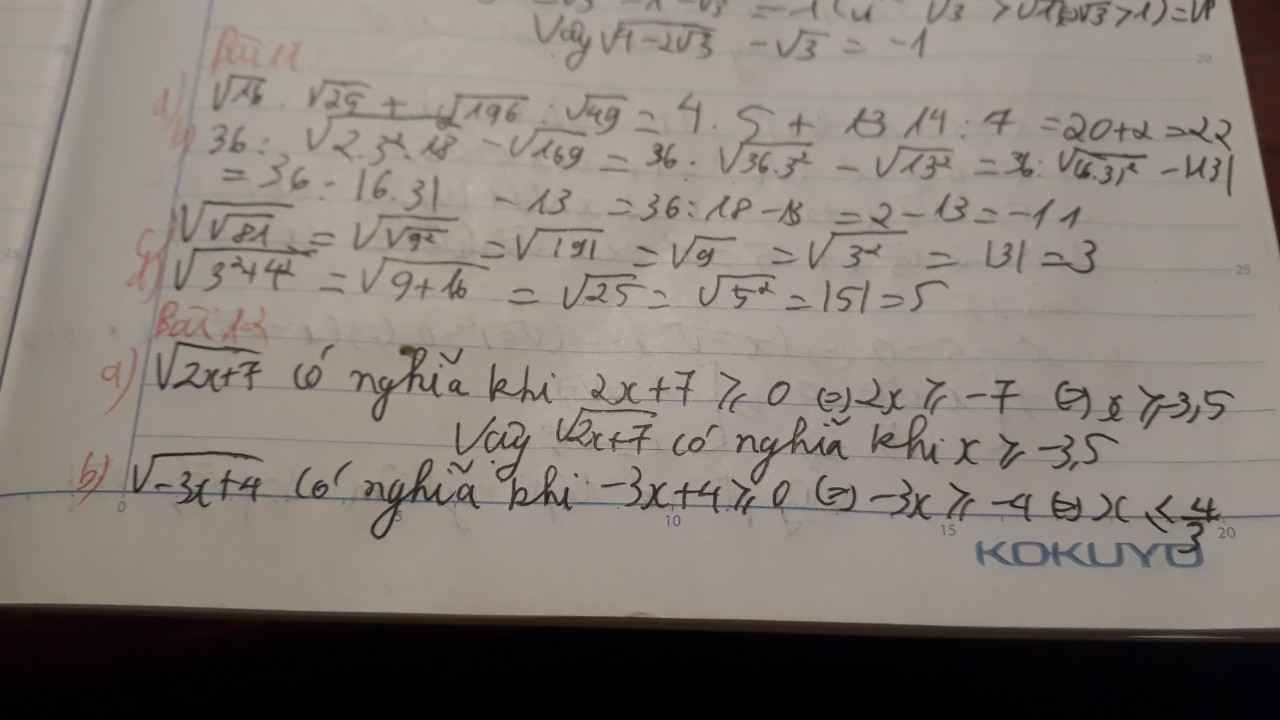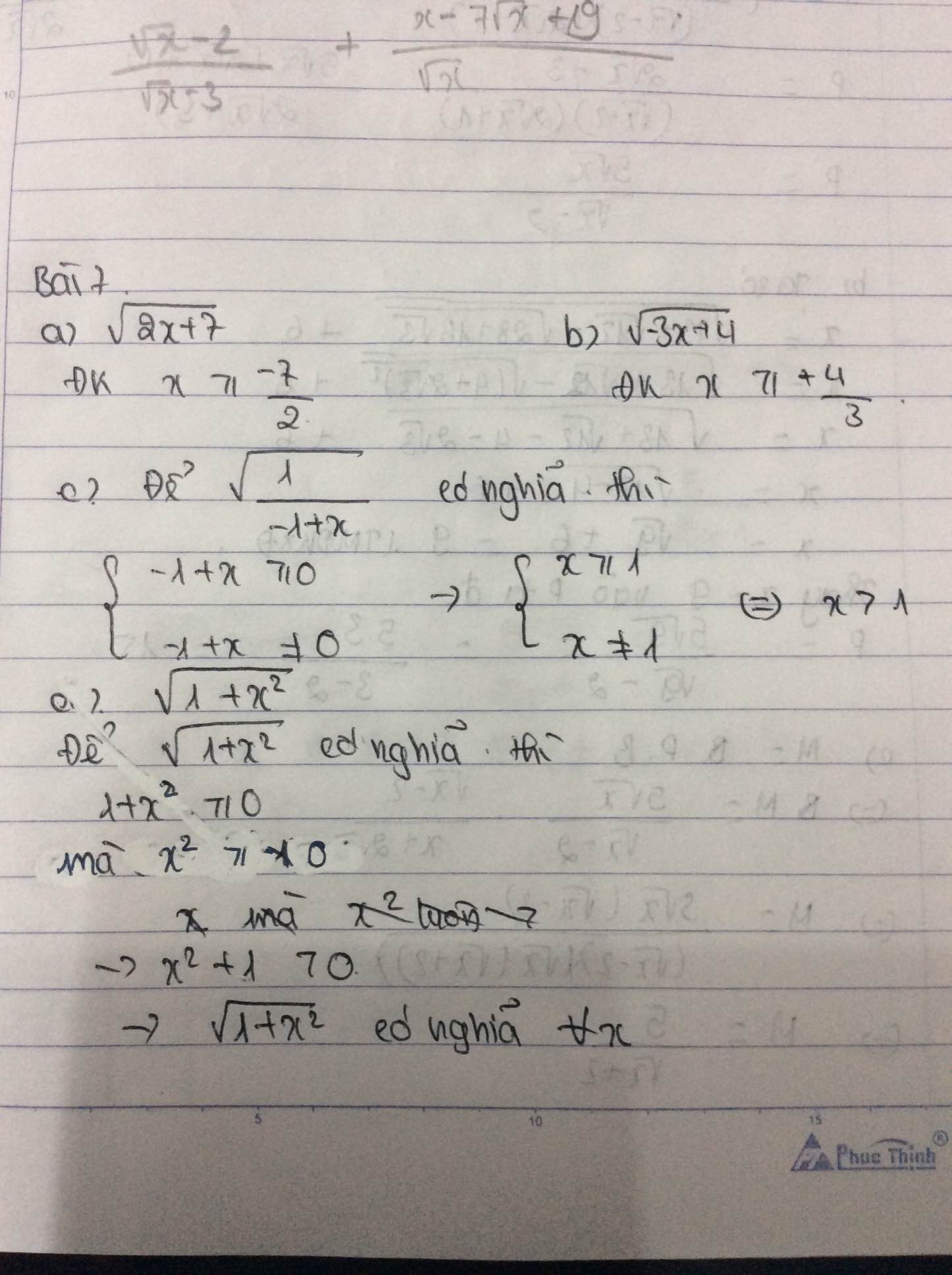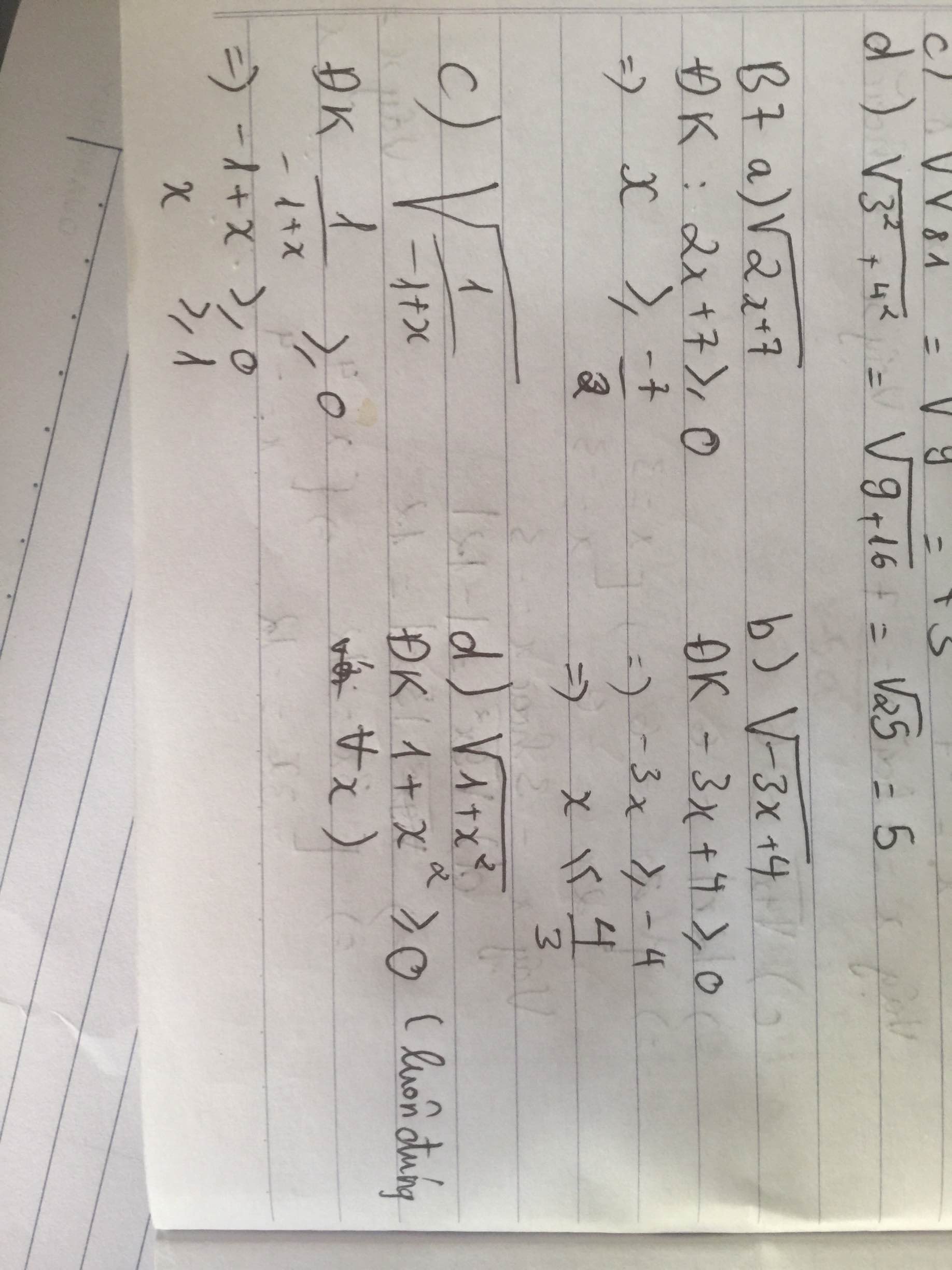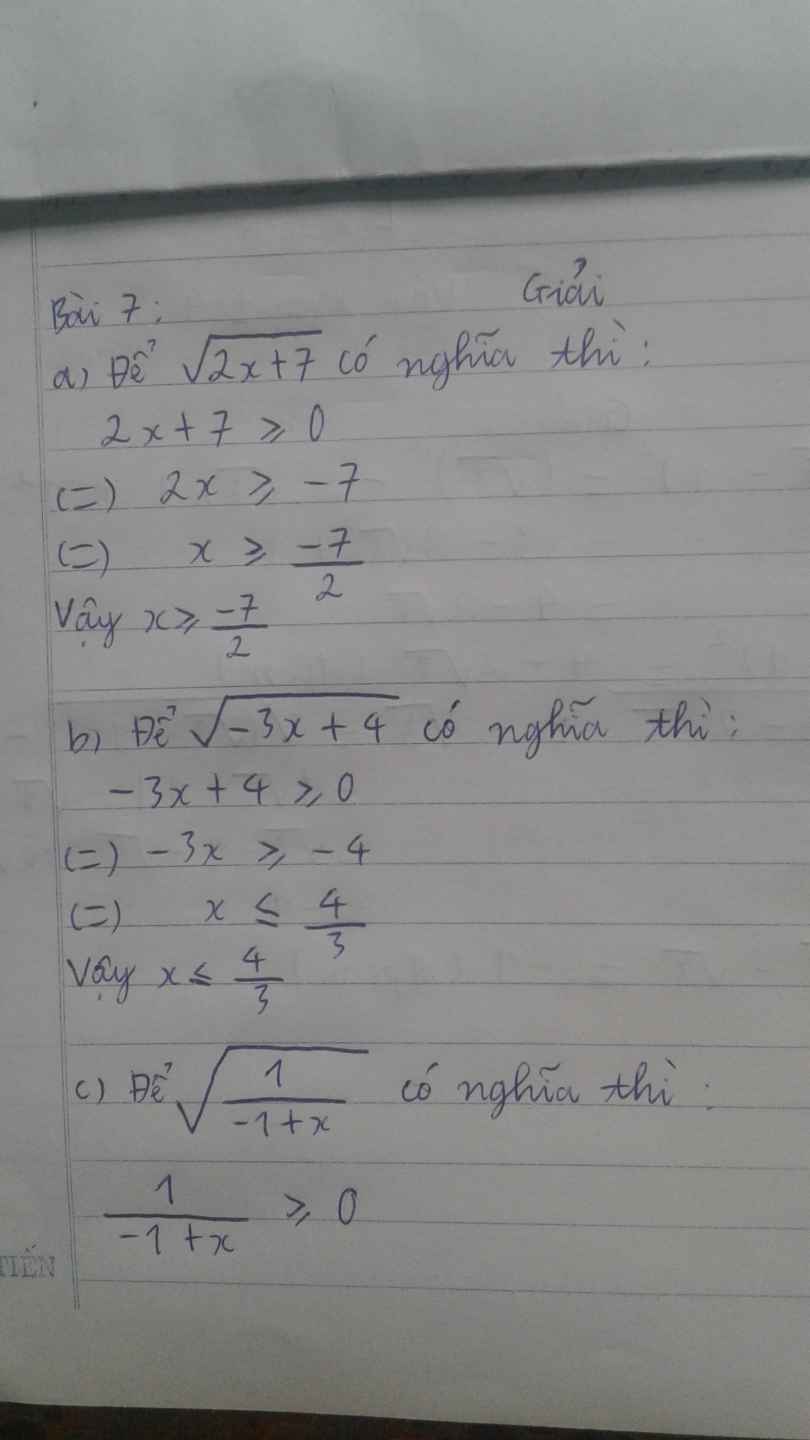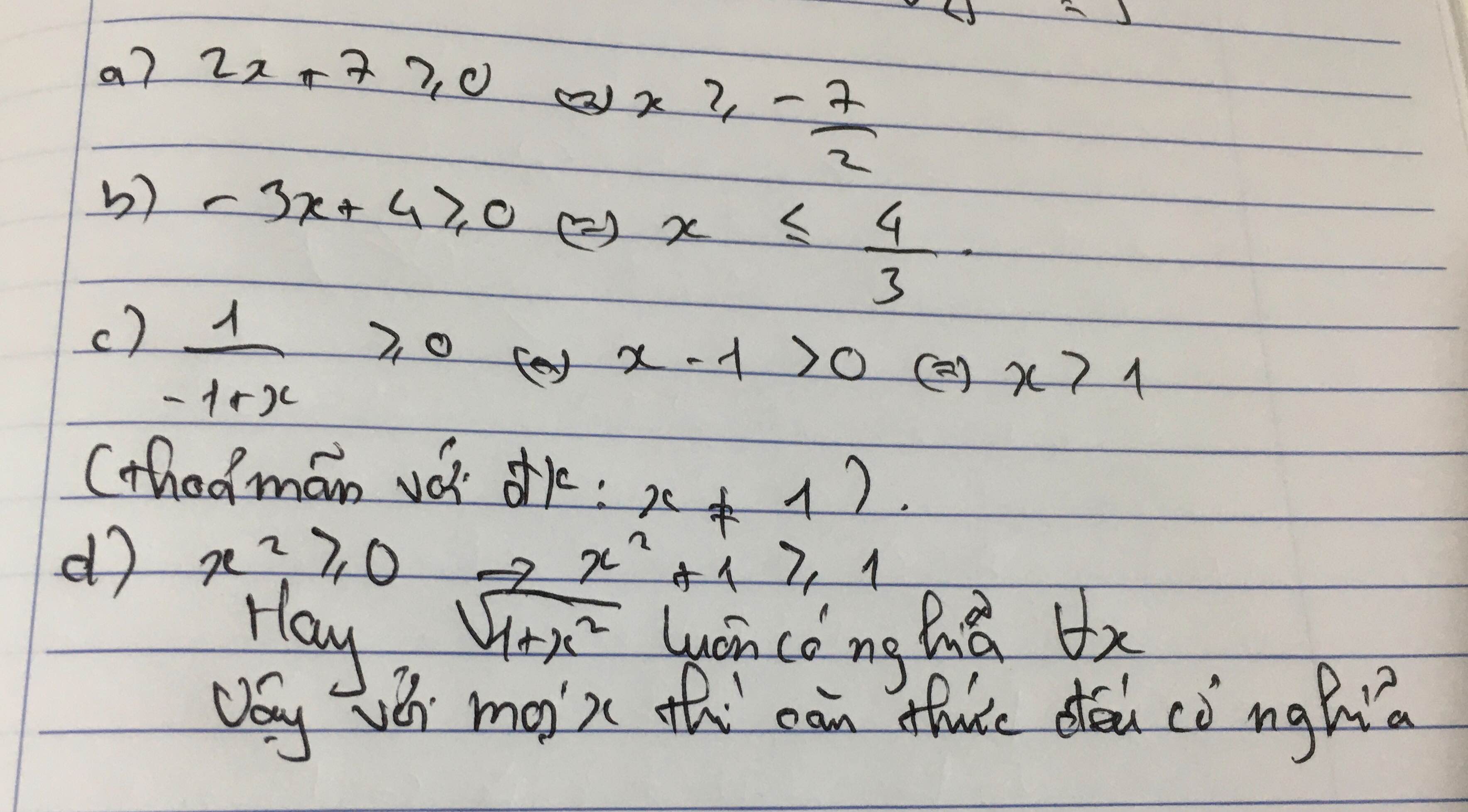a) √2x+7
Để √2x+7 có nghĩa⇔2x+7≥0
⇔2x≥-7
⇔x≥−7/2
b) √−3x+4
Để √−3x+4 có nghĩa ⇔-3x+4≥≥0
⇔-3x≥-4
⇔x≤4/3
c)√1/−1+x1
Để √1/−1+x có nghĩa ⇔1/−1+x≥0
⇔-1+x>0
⇔x>1
d) √1+x21+x2
Ta có x2+1≥≥1>0;∀x∈R
Vậy x∈R
+a) \(\sqrt{2x+7}\) co nghia khi 2x+7≥0⇒x≥\(\dfrac{-7}{2}\)
b) \(\sqrt{-3x+4}\) co nghia khi -3x+4≥0⇒x≤\(\dfrac{4}{3}\)
c) \(\sqrt{\dfrac{1}{-1+x}}\) cp nghia khi \(\dfrac{1}{-1+x}\)≥0 ⇒-1+x>0⇒x>1
d) \(\sqrt{1+x^2}\) co nghia khi 1+x2 ≥0 ma \(x^2\)≥0⇒\(x^2\) + 1≥1>0 vs moi x
a, Để √(2x+7) xác định thì 2x+7 ≥ 0 <=> x ≥ -7/2
b, Để √(-3x+4) xác định thì 4-3x ≥ 0 <=> 4/3 ≥ x
c, √(1/-1+x) xác định thì 1/-1+x ≥ 0 <=> x-1 >0 <=> x> 1
d, √(1+x^2) xác định thì 1+x^2 ≥ 0 mà x^2 ≥0 <=> x^2+1 ≥ 1 ( T/mãn)
a) x\(\ge\dfrac{-7}{2}\)
b) x\(\le\dfrac{4}{3}\)
c) x>1
d) \(x\in R\)
a. \(\sqrt{2x+7}\) có nghĩa khi 2x + 7 ≥ 0 ⇒x ≥ \(\dfrac{-7}{2}\)
b. \(\sqrt{-3x+4}\) có nghĩa khi -3x + 4 ≥ 0 ⇒ x ≤ \(\dfrac{4}{3}\)
c. \(\sqrt{\dfrac{1}{-1+x}}\) có nghĩa khi 1 + x > 0 ⇒ x > 1
d. \(\sqrt{1+x^2}\) có nghĩa khi 1 + x2 ≥ 0
mà x2 ≥ 0 ⇒ x2 + 1 ≥ 1 > 0 với mọi x
vậy \(\sqrt{1+x^2}\) có nghĩa với mọi x
a) có nghĩa khi:
b) có nghĩa khi:
có nghĩa khi:
d) có nghĩa khi:
Mà với mọi
Vậy có nghĩa với mọi
a) 2x + 7 ≥ 0 ⇔ 2x ≥ -7 ⇔ x ≥ \(-\dfrac{7}{2}\)
b) -3x + 4 ≥ 0 ⇔ -3x ≥ -4 ⇔ x ≤ \(\dfrac{4}{3}\)
c) -1 + x > 0 ⇔ x > 1
d) 1 + x2 > 0 ∀ x
a) có nghĩa khi:
.
b) có nghĩa khi:
.
có nghĩa khi:
.
d) có nghĩa khi:
Mà với mọi .
Vậy có nghĩa với mọi .
a) có nghĩa khi:
.
b) có nghĩa khi:
.
có nghĩa khi:
.
d) có nghĩa khi:
Mà với mọi .
Vậy có nghĩa với mọi .
a) Ta có:
có nghĩa khi và chỉ khi:
.
b) Ta có
có nghĩa khi và chỉ khi:
c) Ta có:
có nghĩa khi và chỉ khi:
d)
Ta có: , với mọi số thực
, (Cộng cả 2 vế của bất đẳng thức trên với )
, mà
Vậy căn thức trên luôn có nghĩa với mọi số thực .
a) Ta có:
có nghĩa khi và chỉ khi:
.
b) Ta có
có nghĩa khi và chỉ khi:
c) Ta có:
có nghĩa khi và chỉ khi:
d)
Ta có: , với mọi số thực
, (Cộng cả 2 vế của bất đẳng thức trên với )
, mà
Vậy căn thức trên luôn có nghĩa với mọi số thực .
a) \(\sqrt{2x+7}\) có nghĩa khi 2x + 7 ≥ 0 ⇔ 2x ≥ -7 ⇔ x ≥ \(\dfrac{-7}{2}\)
Với x ≥ \(\dfrac{-7}{2}\) thì \(\sqrt{2x+7}\) có nghĩa
b) \(\sqrt{-3x+4}\) có nghĩa khi -3x + 4 ≥ 0 ⇔ -3x ≥ -4 ⇔ x ≤ \(\dfrac{4}{3}\)
Với x ≤ \(\dfrac{4}{3}\) thì \(\sqrt{-3x+4}\) có nghĩa
a) \(\sqrt{2x+7}\) có nghĩa khi 2x+7 ≥ 0 ⇔ 2x ≥ -7 ⇔ x ≥ \(\dfrac{-7}{2}\)
b) \(\sqrt{-3x+4}\) có nghĩa khi -3x+4 ≥ 0 ⇔ -3x ≥ -4 ⇔ x ≤ \(\dfrac{4}{3}\)
c) \(\sqrt{\dfrac{1}{-1+x}}\) có nghĩa khi \(\dfrac{1}{-1+x}\ge0\) ⇔ -1+x \(\ge\) 0 ⇔ x ≥ 1
d) \(\sqrt{1+x^2}\) có nghĩa khi 1+x2 ≥ 0 mà x2 luôn ≥ 0 với mọi x nên \(\sqrt{1+x^2}\) có nghĩa với mọi x
a) \(\sqrt{2x+7}\) có nghĩa khi :
2x + 7 \(\ge\) 0 \(\Rightarrow\) x \(\ge\) \(\dfrac{-7}{2}\)
b) \(\sqrt{-3x+4}\) có nghĩa khi :
- 3x + 4 \(\ge\) 0 \(\Rightarrow\) x \(\le\) \(\dfrac{4}{3}\)
c) \(\sqrt{\dfrac{1}{-1+x}}\) có nghĩa khi :
\(\dfrac{1}{-1+x}\) \(\ge\) 0 \(\Rightarrow\) -1 + x > 0 \(\Rightarrow\) x > 1
d) \(\sqrt{1+x^2}\) có nghĩa khi :
1 + x\(^2\) \(\ge\) 0
Mà x\(^2\) \(\ge\) 0 \(\Rightarrow\) x\(^2\) + 1 \(\ge\) 1 > 0 với mọi x.
Vậy \(\sqrt{1+x^2}\) có nghĩa với mọi x