Hmm theo mình là không nhé vì AB không song song DC.
Đúng bạn nhé.
hình vẽ hơi lệch . còn lại thì đúng
Hmm theo mình là không nhé vì AB không song song DC.
Đúng bạn nhé.
hình vẽ hơi lệch . còn lại thì đúng
Tam giác ABC có đáy BC cố định và dài 4cm. Đỉnh A di chuyển trên đường thẳng d (\(d\perp BC\)). Gọi H là chân đường cao hạ từ đỉnh A xuống đường thẳng BC
a) Điền vào ô trống trong bảng sau :
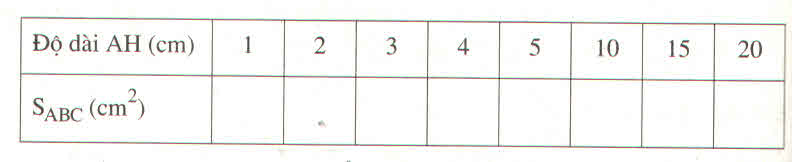
b) Vẽ đồ thị biểu diễn số đo \(S_{ABC}\) độ dài AH
c) Diện tích tam giác ABC có tỉ lệ thuận với chiều cao AH không ?
1) Cho \(\Delta ABC\), M là trung điểm trong \(\Delta ABC;AD\perp BC\equiv D;BE\perp AC\equiv E;CF\perp AB\equiv F\). Qua M kẻ các đường thẳng \(//AD,\cap BC\equiv H;//BE,\cap AC\equiv K;//CF,\cap AB\equiv I\)
CMR: \(\dfrac{MH}{AD}+\dfrac{MK}{BE}+\dfrac{MI}{CF}=1\)
2) Cho \(\Delta ABC\), trung tuyến BD, CE cắt nhau tại G, BD=10cm, CE=12cm
a) CMR: \(\Delta BMC\) vuông
b) \(S_{ABC}=?\)
Tam giác PAF được vẽ trên giấy kẻ ô vuông (h.135)
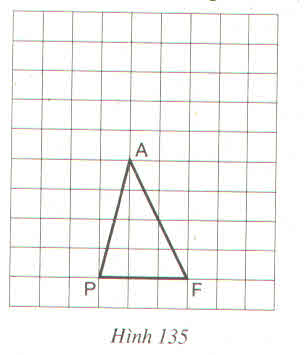
Hãy chỉ ra :
a) Một điểm I sao cho \(S_{PIF}=S_{PAF}\)
b) Một điểm O sao cho \(S_{POF}=2.S_{PAF}\)
c) Một điểm N sao cho \(S_{PNF}=\dfrac{1}{2}S_{PAF}\)
Mọi người giúp mình câu này với:
Cho \(\Delta ABC\). Chứng minh rằng: \(S_{abc}\le\frac{\sqrt{3}}{12}\cdot\left(AB^2+BC^2+CA^2\right)\)
Cho tam giác ABC. Hãy chỉ ra một số vị trí của điểm M nằm trong tam giác đó sao cho :
\(S_{AMB}+S_{BMC}=S_{MAC}\)
cho ΔABC đều, cạnh là a. tính \(S_{ABC}\)theo a.
Cho tam giác HJI có đường cao HM tam giác KIJ có đường cao KL Chứng minh rằng \(\dfrac{S_{HIJ}}{S_{KIJ}}=\dfrac{HM}{KL}\)
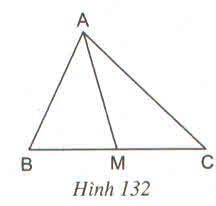
Cho tam giác ABC và đường trung tuyến AM (h.132)
Chứng minh :
\(S_{AMB}=S_{AMC}\)
a) Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S' là diện tích của tam giác DBC
Chứng minh rằng : \(\dfrac{S'}{S}=\dfrac{DK}{AH}\)
b) Cho tam giác ABC và điểm M bất kì nằm trong tam giác đó. Kẻ các đường cao của tam giác đó là AD, BE và CF. Đường thẳng đi qua điểm M và song song với AD cắt cạnh BC tại điểm H. Đường thẳng đi qua điểm M và song song với BE cắt cạnh AC tại điểm K. Đường thẳng đi qua điểm M và song song với CF cắt cạnh BA tại điểm T
Chứng minh rằng \(\dfrac{MH}{AD}+\dfrac{MK}{BE}+\dfrac{MT}{CF}=\)