Nguyễn Văn Đạt: sai oy
Vẽ hình như Đạt nhé.
Theo Pytago ta có: \(AH=\sqrt{AB^2-BH^2}=\sqrt{a^2-\left(\frac{a}{2}\right)^2}=\sqrt{\frac{3a^2}{4}}=\frac{a\sqrt{3}}{2}\)
Khi đó: \(S_{ABC}=\frac{1}{2}\cdot AH\cdot BC=\frac{1}{2}\cdot\frac{a\sqrt{3}}{2}\cdot a=\frac{a^2\sqrt{3}}{4}\)
Vậy...
Mình là hình này làm minh họa nhé :
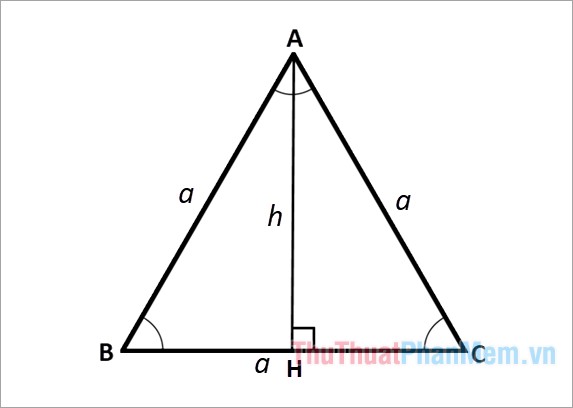
Kẻ \(AH\perp BC\)
Do \(\Delta ABC\) đều mà \(AH\) là đường cao nên \(AH\) đồng thời là trung tuyến.
\(\Rightarrow BH=CH=\frac{BC}{2}=\frac{a}{2}\)
Khi đó : \(S_{ABC}=\frac{1}{2}AH.BC=\frac{1}{2}\cdot\frac{a}{2}\cdot a=\frac{a^2}{4}\)
Vậy : \(S_{ABC}=\frac{a^2}{4}\).