Bài 3: Diện tích tam giác
Các câu hỏi tương tự
a) Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S là diện tích của tam giác DBC
Chứng minh rằng : dfrac{S}{S}dfrac{DK}{AH}
b) Cho tam giác ABC và điểm M bất kì nằm trong tam giác đó. Kẻ các đường cao của tam giác đó là AD, BE và CF. Đường thẳng đi qua điểm M và song song với AD cắt cạnh BC tại điểm H. Đường thẳng đi qua điểm M và song song với BE cắt cạnh AC tại điểm K. Đường thẳng đi qua điểm M và son...
Đọc tiếp
a) Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S' là diện tích của tam giác DBC
Chứng minh rằng : \(\dfrac{S'}{S}=\dfrac{DK}{AH}\)
b) Cho tam giác ABC và điểm M bất kì nằm trong tam giác đó. Kẻ các đường cao của tam giác đó là AD, BE và CF. Đường thẳng đi qua điểm M và song song với AD cắt cạnh BC tại điểm H. Đường thẳng đi qua điểm M và song song với BE cắt cạnh AC tại điểm K. Đường thẳng đi qua điểm M và song song với CF cắt cạnh BA tại điểm T
Chứng minh rằng \(\dfrac{MH}{AD}+\dfrac{MK}{BE}+\dfrac{MT}{CF}=\)
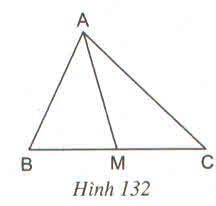
Cho tam giác ABC và đường trung tuyến AM (h.132)
Chứng minh :
\(S_{AMB}=S_{AMC}\)
Tam giác PAF được vẽ trên giấy kẻ ô vuông (h.135)
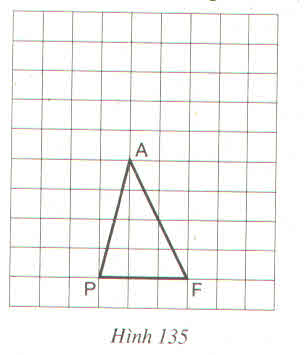
Hãy chỉ ra :
a) Một điểm I sao cho \(S_{PIF}=S_{PAF}\)
b) Một điểm O sao cho \(S_{POF}=2.S_{PAF}\)
c) Một điểm N sao cho \(S_{PNF}=\dfrac{1}{2}S_{PAF}\)
Cho tam giác ABC vuông tại A (AB<AC) có đường cao AH, biết AB=12cm, AC=16cm
a) Tính BC và AH
b) Chứng minh tam giác BHA đồng dạng tam giác ABC
Tam giác ABC có đáy BC cố định và dài 4cm. Đỉnh A di chuyển trên đường thẳng d (dperp BC). Gọi H là chân đường cao hạ từ đỉnh A xuống đường thẳng BC
a) Điền vào ô trống trong bảng sau :
b) Vẽ đồ thị biểu diễn số đo S_{ABC} độ dài AH
c) Diện tích tam giác ABC có tỉ lệ thuận với chiều cao AH không ?
Đọc tiếp
Tam giác ABC có đáy BC cố định và dài 4cm. Đỉnh A di chuyển trên đường thẳng d (\(d\perp BC\)). Gọi H là chân đường cao hạ từ đỉnh A xuống đường thẳng BC
a) Điền vào ô trống trong bảng sau :
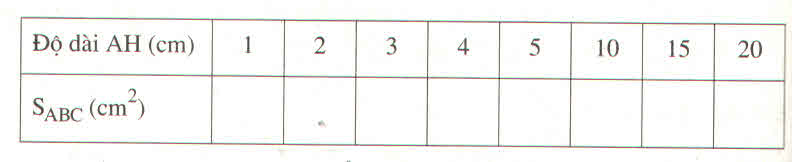
b) Vẽ đồ thị biểu diễn số đo \(S_{ABC}\) độ dài AH
c) Diện tích tam giác ABC có tỉ lệ thuận với chiều cao AH không ?
Cho tam giác ABC. Hãy chỉ ra một số vị trí của điểm M nằm trong tam giác đó sao cho :
\(S_{AMB}+S_{BMC}=S_{MAC}\)
Cho tam giác ABC vuông tại A, AB = a , AC = b , đường cao AH. Ở phía ngoài tam giác vẽ các hình vuông ABDE, ACFG, BCIK.
a) Tính diện tích tam giác DBC.
b) Chứng minh rằng AK = DC .
c) Đường thẳng AH cắt KI ở M. Tính diện tích các tứ giác BHMK, CHMI, BCIK .
Ai giúp em với chiều em học r ạ
Cho tam giác ABC có đáy BC cố định và đỉnh A di động trên một đường thẳng d cố định song song với đường thẳng BC. Chứng minh rằng tam giác ABC luôn có diện tích không đổi ?







