Các câu hỏi tương tự
Cho ba tia Ox, Oy, Oz vuông góc với nhau từng đôi một và ba điểm A
∈
Ox, B
∈
Oy, C
∈
Oz sao cho OAOBOCa. Khẳng định nào sau đây là sai: A.
S
△
A
B
C
a
2
2
B.
O
C
⊥
O...
Đọc tiếp
Cho ba tia Ox, Oy, Oz vuông góc với nhau từng đôi một và ba điểm A ∈ Ox, B ∈ Oy, C ∈ Oz sao cho OA=OB=OC=a. Khẳng định nào sau đây là sai:
A. S △ A B C = a 2 2
B. O C ⊥ O A B
C. v O A B C = a 3 6
D. O A B C là hình chóp đều
Cho ba tia Ox, Oy, Oz đôi một vuông góc với nhau. Gọi C là điểm cố định trên Oz, đặt OC1, các điểm A,B thay đổi trên Ox, Oy sao cho OA+OBOC. Tìm giá trị bé nhất của bán kính mặt cầu ngoại tiếp tứ diện OABC
Đọc tiếp
Cho ba tia Ox, Oy, Oz đôi một vuông góc với nhau. Gọi C là điểm cố định trên Oz, đặt OC=1, các điểm A,B thay đổi trên Ox, Oy sao cho OA+OB=OC. Tìm giá trị bé nhất của bán kính mặt cầu ngoại tiếp tứ diện OABC
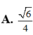
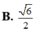
![]()
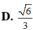
Cho ba tia Ox, Oy, Oz đôi một vuông góc với nhau. Gọi C là điểm cố định trên Oz, đặt OC1 các điểm A, B thay đổi trên Ox, Oy sao cho OA+OBOC. Giá trị bé nhất của bán kính mặt cầu ngoại tiếp tứ diện OABC là A.
6
3
B.
6
C.
6
4
D. ...
Đọc tiếp
Cho ba tia Ox, Oy, Oz đôi một vuông góc với nhau. Gọi C là điểm cố định trên Oz, đặt OC=1 các điểm A, B thay đổi trên Ox, Oy sao cho OA+OB=OC. Giá trị bé nhất của bán kính mặt cầu ngoại tiếp tứ diện OABC là
A. 6 3
B. 6
C. 6 4
D. 6 2
Cho điểm M (1; 2; 5), mặt phẳng (P) đi qua điểm M cắt trục tọa độ Ox; Oy; Oz tại A, B, C sao cho M là trực tâm của tam giác ABC. Phương trình mặt phẳng (P) là
Đọc tiếp
Cho điểm M (1; 2; 5), mặt phẳng (P) đi qua điểm M cắt trục tọa độ Ox; Oy; Oz tại A, B, C sao cho M là trực tâm của tam giác ABC. Phương trình mặt phẳng (P) là
![]()
![]()
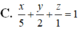
![]()
Viết phương trình tổng quát của mặt phẳng
α
qua ba điểm A, B, C lần lượt là hình chiếu của điểm M(2;3;-5) xuống các trục Ox, Oy, Oz. A. 15x-10y-6z-300 B. 15x-10y-6z+300 C. 15x+10y-6z+300 D. 15x+10y-6z-300
Đọc tiếp
Viết phương trình tổng quát của mặt phẳng α qua ba điểm A, B, C lần lượt là hình chiếu của điểm M(2;3;-5) xuống các trục Ox, Oy, Oz.
A. 15x-10y-6z-30=0
B. 15x-10y-6z+30=0
C. 15x+10y-6z+30=0
D. 15x+10y-6z-30=0
Trong không gian cho ba tia Ox,Oy,Oz đôi một vuông góc và các điểm A,B,C không trùng với O lần lượt thay đổi trên các tia Ox,Oy,Oz và luôn thoả mãn điều kiện: tỉ số giữa diện tích tam giác ABC và thể tích khối tứ diện OABC bằng
3
2
Khối diện OABC có thể tích nhỏ nhất bằng
Đọc tiếp
Trong không gian cho ba tia Ox,Oy,Oz đôi một vuông góc và các điểm A,B,C không trùng với O lần lượt thay đổi trên các tia Ox,Oy,Oz và luôn thoả mãn điều kiện: tỉ số giữa diện tích tam giác ABC và thể tích khối tứ diện OABC bằng 3 2 Khối diện OABC có thể tích nhỏ nhất bằng
![]()
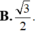
![]()
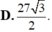
Mặt phẳng (P) thay đổi luôn đi qua M (1; 2; 3). Biết (P) cắt các tia Ox, Oy, Oz tại A, B, C. Tìm GTNN của thể tích OABC (Vmin).
A. Vmin = 24.
B. Vmin = 27.
C. Vmin = 9 14
D. Vmin = 36.
Lập phương trình của mặt phẳng (α) đi qua điểm M(1; 2; 3) và cắt ba tia Ox, Oy, Oz lần lượt tại A, B, C sao cho thể tích tứ diện OABC nhỏ nhất.
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) chứa điểm M (1; 3; -2), cắt các tia Ox, Oy, OZ lần lượt tại A, B, C sao cho
O
A
1
O
B
2
O
C
4
A
.
2
x
-...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) chứa điểm M (1; 3; -2), cắt các tia Ox, Oy, OZ lần lượt tại A, B, C sao cho O A 1 = O B 2 = O C 4
A . 2 x - y - z - 1 = 0
B . x + 2 y + 4 z + 1 = 0
C . 4 x + 2 y + z + 1 = 0
D . 4 x + 2 y + z - 8 = 0
Cho
M
3
;
4
;
5
. Gọi A, B, C là hình chiếu vuông góc của M xuống các trục tọa độ Ox, Oy, Oz. Tính tổng
T
M
A
2
+
M
B
2
+
M
C
2
.
Đọc tiếp
Cho M 3 ; 4 ; 5 . Gọi A, B, C là hình chiếu vuông góc của M xuống các trục tọa độ Ox, Oy, Oz. Tính tổng T = M A 2 + M B 2 + M C 2 .
![]()
![]()
![]()
![]()


