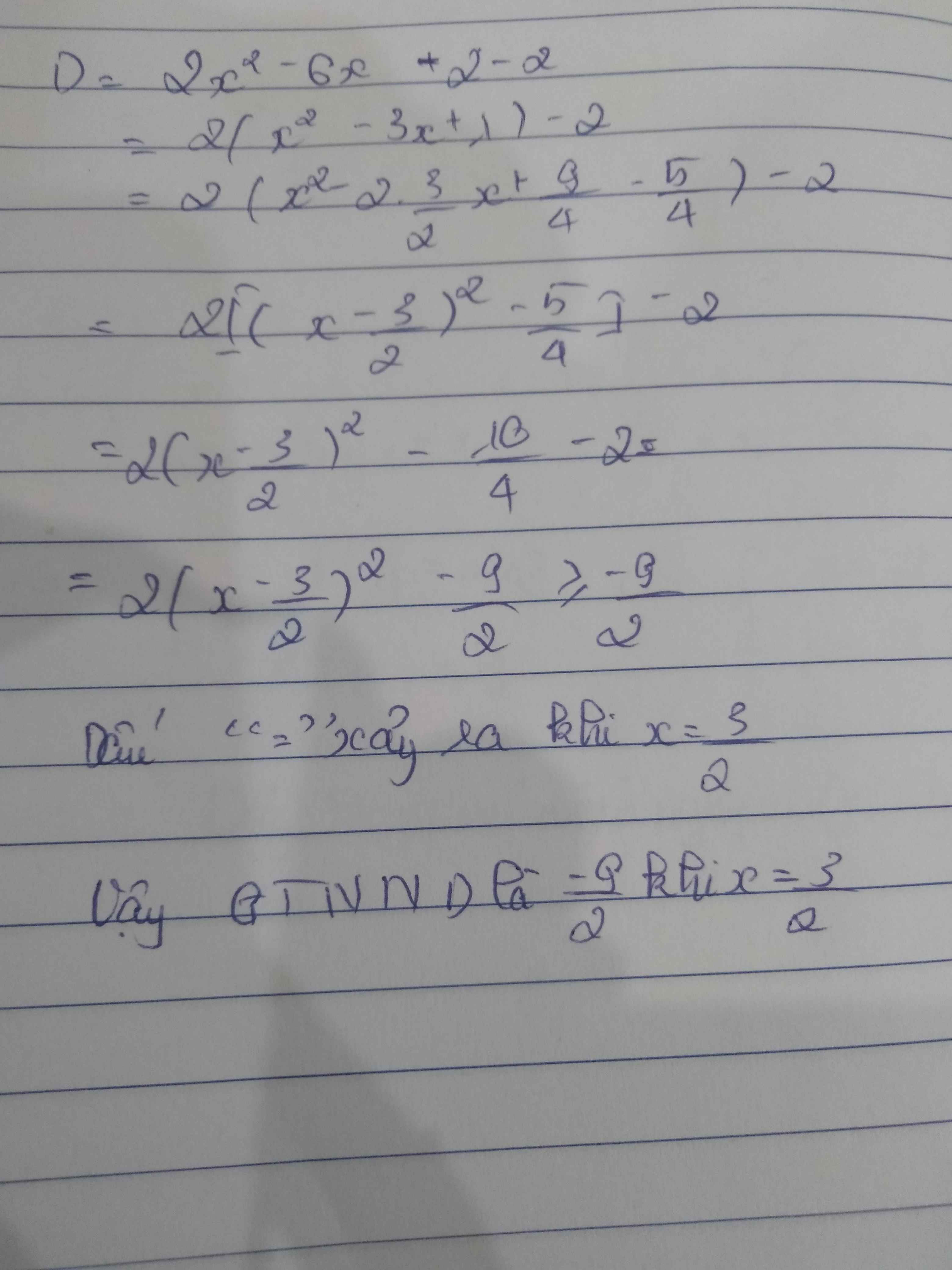D= 2x2 - 6x
= 2(x2 - 3x +\(\dfrac{9}{4}\)) - \(\dfrac{9}{2}\)
= 2[x2 - 2.x.\(\dfrac{3}{2}\) + (\(\dfrac{3}{2}\))2 ] - \(\dfrac{9}{2}\)
= 2 (x - \(\dfrac{3}{2}\))2 - \(\dfrac{9}{2}\)
Ta có:
2(x - \(\dfrac{3}{2}\))2 ≥ 0 ⇒ 2 (x - \(\dfrac{3}{2}\))2 - \(\dfrac{9}{2}\) ≥ -\(\dfrac{9}{2}\)
Hay D≥ -\(\dfrac{9}{2}\)
Dấu = xảy ra ⇔ (x - \(\dfrac{3}{2}\)) = 0 ⇔ x = \(^{\dfrac{3}{2}}\)
Vậy MinD = - \(\dfrac{9}{2}\) ⇔ x = \(\dfrac{3}{2}\)