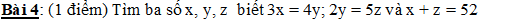Question

2/x=3/y

Tìm x,y biết xy=96

Ai giúp em ạ. ai giải đáp dễ hiểu em sẽ tick

Answer 1

\(\frac{2}{x}=\frac{3}{y}\)

\(\Rightarrow3x=2y\)

\(\Rightarrow x=\frac{2y}{3}\)

Thay x vào xy ( đề bài ) ta có :

\(\frac{2y}{3}\cdot y=96\)

\(\Rightarrow\frac{2y^2}{3}=96\)

\(\Rightarrow2y^2=288\)

\(\Rightarrow y^2=144\)

\(\Rightarrow y=\left\{\pm12\right\}\)

\(\Rightarrow\orbr{\begin{cases}y=12\Rightarrow x=8\\y=-12\Rightarrow-8\end{cases}}\)

Vậy các cặp ( x; y ) thỏa mãn là ( 8; 12 ) và ( -8; -12 )

Answer 2

vao nink này nha

Answer 3

Áp dụng công thức dãy tỉ số bằng nhau:

x/2 = y/3 = xy/2.3 = 96/6 = 16

x/2 =16 => x=32

y/3 =16 => y=48

Answer 4

     2/x = 3/y

<=> 2y = 3x

<=> 2yx = 3xx         

<=> 2.96 = 3.x² 

<=> 192 = 3.x² 

<=> x²    = 192 : 3

<=>   x²  = 64

<=>   x²  = 8² 

<=>    x   = 8 

 => y = 96 : 8

     y = 12

  Vậy x = 8

         y = 12

                 ~Hok tốt~ 

Answer 5

ta có \(\frac{2}{x}=\frac{3}{y}=2.y=3x=\frac{y}{3}=\frac{x}{2}\)

Đặt \(\frac{y}{3}=\frac{x}{2}=k\)=> y = 3.k , x = 2.k

ta có 3k . 2k = 96  => 6K² = 96 => k² = 16 => k = 4 hoặc - 4

nếu \(\orbr{\begin{cases}\frac{y}{3}=4\Rightarrow y=12\\\frac{y}{3}=-4\Rightarrow y=-12\end{cases}}\)

nếu\(\orbr{\begin{cases}\frac{x}{2}=4\Rightarrow x=8\\\frac{x}{2}=-4\Rightarrow x=-8\end{cases}}\)