1.Cho hình thang ABCD có 2 đáy AB và CD . Điểm M nằm trên nằm trên đoạn thẳng AC sao cho AM = CM;điểm N trên cạnh CD sao cho MN song song với BD . Biết diện tích hình thang ABCD=16cm2.
a) CM : Diện tích hình tam giác BMN bằng diện tích hình tam giác DMN
b) Tính diện tích hình tứ giác ABND
Ai đầu tiên mk k cho !
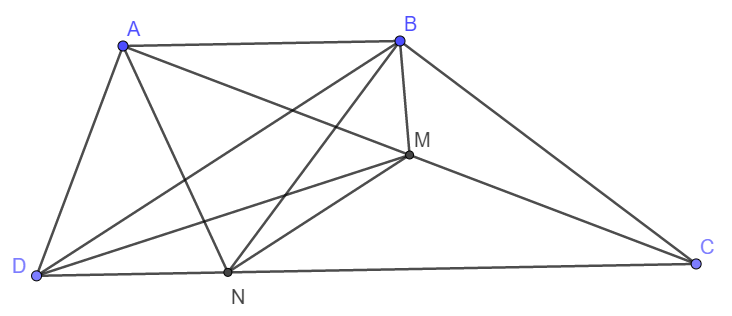
a) Ta thấy hai tam giác MN và DMN có chung cạnh MN.
Lại có do DB // MN nên chiều cao hà từ B và D xuống MN là bằng nhau.
Vậy diện tích tam giác BNM bằng diện tích tam giác DMN.
b) Ta thấy \(AM=MC\Rightarrow\frac{S_{ABM}}{S_{BAC}}=\frac{1}{2};\frac{S_{ADM}}{S_{DAC}}=\frac{1}{2}\)
Vậy nên \(\frac{S_{ABM}+S_{ADM}}{S_{BAC}+S_{DAC}}=\frac{1}{2}\Rightarrow\frac{S_{ABMD}}{S_{ABCD}}=\frac{1}{2}\)
\(\Rightarrow S_{ABMD}=16:2=8\left(cm^2\right)\)
Lại có \(S_{ABMD}=S_{ABMND}-S_{DMN}=S_{ABND}+S_{BMN}-S_{DMN}\)
\(=S_{ABND}\) hay \(S_{ABND}=8cm^2\)
DB//MN có phải gạch // dấu đó ko
Câu a dễ rồi nên t trả lời câu b thôi nha
b) M là trung điểm AC nên SABM = SCMB = SABC :2 ; SADM = SCMD = SADC/2
ta được SAMB + SAMD = SCMB + SCMD = SABC/2 + SADC/2
SABMD =SCMB + SCMD = SABCD :2 =16:2 = 8cm2
SABMD = 8
SABD + SBMD = 8
lại có : MN//BD nên SBMD = SBND ( chứng minh như câu a nha )
ta được : SABD + SBND = 8
SABND = 8cm2











