Các câu hỏi tương tự
Cho tam giác ABC có trung tuyến AM. Gọi H là trực tâm, O là giao điểm các đường trung trực của tam giác ABC. Giao điểm của AM và HO là G. Chứng minh rằng G là trọng tâm của tam giác ABC
Cho tam giác ABC cân tại A. Gọi G là trọng tâm của tam giác, I là giao điểm của các đường phân giác trong tam giác. Khi đó ta có
A. I cách đều ba đỉnh của tam giác ABC
B. A, I, G thẳng hàng
C. G cách đều ba cạnh của tam giác ABC
D. Cả 3 đáp án trên đều đúng
Cho Tam giác ABC cân tại A . Gọi G là trọng tâm của tam giác, I là giao điểm của các đường phân giác trong tam giác. Khi đó ta có A. I cách đều ba đỉnh của tam giác ABC B. A, I, G thẳng hàng C. G cách đều ba cạnh của tam giác ABC D. Cả 3 đáp án trên đều đúng
Đọc tiếp
Cho Tam giác ABC cân tại A . Gọi G là trọng tâm của tam giác, I là giao điểm của các đường phân giác trong tam giác. Khi đó ta có
A. I cách đều ba đỉnh của tam giác ABC
B. A, I, G thẳng hàng
C. G cách đều ba cạnh của tam giác ABC
D. Cả 3 đáp án trên đều đúng
Cho tam giác ABC có trung tuyến AM . Gọi H là trực tâm, O là giao điểm của các đường trung trực của tam giác ABC . Giao điểm của AM và HO là G . CMR : G là trọng tâm của tam giác ABC
Mn nhớ zúp mk nhoa !! Thks nhìu :)) Đúng sẽ tik <33
Cho tam giác ABC cân tại A. Gọi G là trọng tâm của tam giác, gọi I là giao điểm các đường phân giác của tam giác. Chứng minh rằng ba điểm A, G, I thẳng hàng.
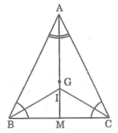
Cho tam giác ABC cân tại A, goi G là trọng tâm của tam giác, gọi I là giao điểm của các đường phân giác của tam giác. Chứng minh rằng 3 điểm A, G, I thẳng hàng. ( nhanh lên mình đang cần lắm )
cho tam giác nhọn ABC, trung tuyến AM. Gọi H là trực tâm, O là giao điểm của các đường trung trực của tam giác ABC. CMR :
a, So sánh AH và OM.
b, gọi G là giao điểm của AM và HO. CMR G là trọng tâm của tam giác ABC
Cho tam giác ABC có 3 đỉnh nằm trên một đường tròn O. Vẽ trực tâm H và trọng tâm G của tam giác. Kẻ đường cao AD. Giao điểm thứ hai của AD với đường tròn tâm O là E. Kẻ đường kính AP. Biết góc BAE bằng Góc BCE.
CMR 1, DH=DE
2, Tứ giác BPCH là hình bình hành
3, G nằm giữa OH, GH và GH = 2 GO
Cho tam giác ABC. Gọi G là trọng tâm tam giác. H là trực tâm tam giác. I là giao điểm 3 đường phân giác. O là điểm cách đều 3 đỉnh tam giác.
Chứng minh rằng: tam giác ABC là tam giác đều khi và chỉ khi các điểm G,H,I,O trùng nhau và ngược lại.













