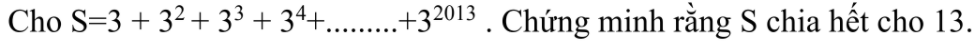Đặt \(A=1+2+4+.........+4096\)
\(2A=2+4+8+......+8192\)
\(\Rightarrow2A-A=8192-1\)
\(\Rightarrow A=8191\)
Đặt \(S=1+2+4+...+1024+2048+4096\)
\(S=1+2^1+2^2+2^3+....+2^{10}+2^{11}+2^{12}\)
\(2S=2+2^2+2^3+....+2^{11}+2^{12}+2^{13}\)
\(2S-S=\left(2+2^2+2^3+....+2^{12}+2^{13}\right)-\left(1+2+2^2+....+2^{11}+2^{12}\right)\)
\(S=2^{13}-1=8192-1=8191\)
A=1+2+4+8+16+.....+1024+2048+4096
2A= 2+4+8+16+32+....+2048+4096+8192
2A-A=A=2+4+8+16+32+....+4096+8192-(1+2+4+8+16+...+1024+2048+4096)
A=8192-1
A=8191 k nha
Theo đầu bài ta có:
\(1+2+4+8+16+32+...+1024+2048+4096\)
\(\Leftrightarrow2^0+2^1+2^2+2^3+2^4+2^5+...+2^{10}+2^{11}+2^{12}\)
\(\Leftrightarrow2\left(2^0+2^1+2^2+...+2^{11}+2^{12}\right)-\left(2^0+2^1+2^2+...+2^{11}+2^{12}\right)\)
\(\Leftrightarrow\left(2^1+2^2+2^3+...+2^{12}+2^{13}\right)-\left(2^0+2^1+2^2+...+2^{11}+2^{12}\right)\)
\(\Leftrightarrow2^{13}-2^0=8192-1=8191\)
A = 1 + 2 + 4 + 8 + 16 + ... + 4096 + 8192
Dễ dàng nhìn thấy:
1 + 2 = 4 - 1 = 3
1 + 2 + 4 = 8 - 1 = 7
1 + 2 + 4 + 8 = 16 - 1 = 15
1 + 2 + 4 + 8 + 16 = 32 - 1 = 31
Theo đó ta thấy được quy luật của tổng trên là: Tổng các số hạng đứng trước sẽ bằng số hạng đứng sau trừ đi 1 đơn vị nên:
1 + 2 + 4 + 8 + 16 + ... + 4096 = 8192 - 1 = 8191
Vậy A = 8191 + 8192 = 16383
1 + 2 + 4 + 8 + 16 + ... + 1024 + 2048 + 4096
Ta có: 1 + 2 = 4 - 1 = 3
1 + 2 + 4 = 8 - 1 = 7
1 + 2 + 4 + 8 = 16 - 1 = 15
Quy luật của tổng trên là: Tổng của các số hạng đứng trước sẽ bằng số hạng đứng sau trừ bớt đi 1 đơn vị. Nên ta có:
1 + 2 + 4 + 8 + 16 + ... + 1024 + 2048 = 4096 - 1 = 4095
Suy ra: 1 + 2 + 4+ 8 + 16 + ... + 1024 + 2048 + 4096 = 4095 + 4096 = 8191