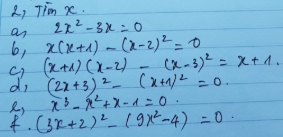1.21:
a: \(x^2-6x=0\)
=>x(x-6)=0
=>\(\left[{}\begin{matrix}x=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\)
b: \(4x\left(x+1\right)=8\left(x+1\right)\)
=>\(x\left(x+1\right)=2\left(x+1\right)\)
=>(x+1)(x-2)=0
=>\(\left[{}\begin{matrix}x+1=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)
c: \(x\left(x-4\right)+\left(x-4\right)^2=0\)
=>\(\left(x-4\right)\left(x+x-4\right)=0\)
=>(x-4)(2x-4)=0
=>2(x-2)(x-4)=0
=>(x-2)(x-4)=0
=>\(\left[{}\begin{matrix}x-2=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=4\end{matrix}\right.\)
d: \(5x\left(x-2\right)-\left(2-x\right)=0\)
=>5x(x-2)+(x-2)=0
=>(x-2)(5x+1)=0
=>\(\left[{}\begin{matrix}x-2=0\\5x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{1}{5}\end{matrix}\right.\)
2.3:
a: \(x^2-6xy+9y^2=x^2-2\cdot x\cdot3y+\left(3y\right)^2=\left(x-3y\right)^2\)
b: \(x^2-9y^2=x^2-\left(3y\right)^2=\left(x-3y\right)\left(x+3y\right)\)
c: \(x^2y^2-4xy+4\)
\(=\left(xy\right)^2-2\cdot xy\cdot2+2^2\)
\(=\left(xy-2\right)^2\)
d: \(y^2-\left(x^2-2x+1\right)\)
\(=y^2-\left(x-1\right)^2\)
\(=\left(y-x+1\right)\left(y+x-1\right)\)
3.4:
a: \(A=2ab-15+3a-10b\)
\(=a\left(2b+3\right)-5\left(2b+3\right)\)
=(2b+3)(a-5)
b: \(B=y^2-z^2+4y+4\)
\(=\left(y^2+4y+4\right)-z^2\)
\(=\left(y+2\right)^2-z^2\)
=(y+2+z)(y+2-z)
c: \(C=x^2+2x-xy-2y\)
=x(x+2)-y(x+2)
=(x+2)(x-y)
d: \(D=4x^2-9y^2+4x-6y\)
\(=\left(2x-3y\right)\left(2x+3y\right)+2\left(2x-3y\right)\)
\(=\left(2x-3y\right)\left(2x+3y+2\right)\)











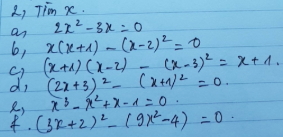 Không làm tắt
Không làm tắt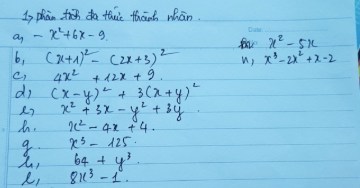 Ko làm tắt
Ko làm tắt