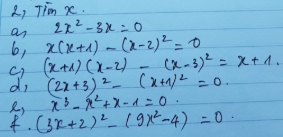Bài 1:
a) \(x^2+4x+4=\left(x+2\right)^2\)
b) \(x^2y^2-6xy+9=\left(xy-3\right)^2\)
c) \(x^4-16y^2=\left(x^2-4y\right)\left(x^2+4y\right)\)
d) \(81-y^4=\left(9-y^2\right)\left(9+y^2\right)=\left(y^2+9\right)\left(3-y\right)\left(3+y\right)\)
e) \(125x^3-8=\left(5x-2\right)\left(25x^2+10x+4\right)\)
f) \(x^3-3x^2+3x-1=\left(x-1\right)^3\)
g) \(1+9x+27x^2+27x^3=\left(1+3x\right)^3\)
h) \(64x^3+1=\left(4x+1\right)\left(16x^2-4x+1\right)\)
i) \(216x^3-125=\left(6x-5\right)\left(36x^2+30x+25\right)\)
k) \(x^2+10x+25=\left(x+5\right)^2\)
l) \(49-36y^2=\left(7-6y\right)\left(7+6y\right)\)
m) \(9x^2-x+\dfrac{1}{36}=\left(3x-\dfrac{1}{6}\right)^2\)
Bài 1:
a, \(x^2+4+4x=x^2+4x+4=\left(x+2\right)^2\)
b, \(-6xy+9+x^2y^2=x^2y^2-6xy+9=\left(xy-3\right)^2\)
c, \(x^4-16y^2=\left(x^2+4y\right)\left(x^2-4y\right)=\left(x^2+4y\right)\left(x+2\sqrt{y}\right)\left(x-2\sqrt{y}\right)\)
d, \(81-y^4=\left(9-y^2\right)\left(9+y^2\right)=\left(3-y\right)\left(3+y\right)\left(9+y^2\right)\)
e, \(125x^3-8=\left(5x\right)^3-2^3=\left(5x-2\right)\left(25x^2+10x+4\right)\)
f, \(x^3-1+3x-3x^2=x^3-3x^2+3x-1=\left(x-1\right)^3\)
Bài 4:
a) Ta có: \(\left(x-2\right)\left(x^2+2x+4\right)-x\left(x^2-1\right)=15\)
\(\Leftrightarrow x^3-8-x^3+x=15\)
\(\Leftrightarrow x-8=15\)
hay x=23
b) Ta có: \(\left(x+1\right)^2-\left(x-2\right)^2=16\)
\(\Leftrightarrow x^2+2x+1-x^2+4x-4=16\)
\(\Leftrightarrow6x=19\)
hay \(x=\dfrac{19}{6}\)
c) Ta có: \(\left(2x+3\right)^2-5\left(2x+3\right)=0\)
\(\Leftrightarrow\left(2x+3\right)\left(2x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-3}{2}\\x=1\end{matrix}\right.\)
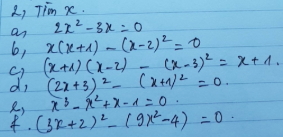Không làm tắt
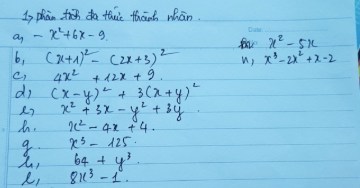Ko làm tắt
