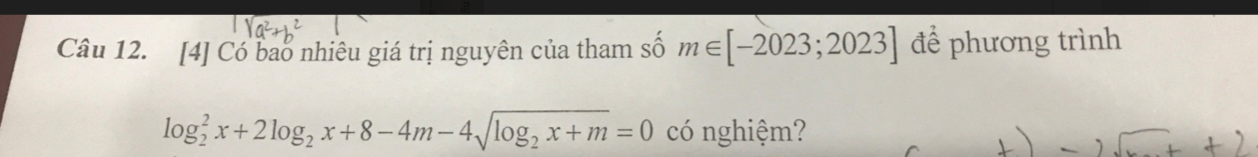ĐK: \(\left\{{}\begin{matrix}x>0\\\log_2x+m\ge0\end{matrix}\right.\)
\(pt\Leftrightarrow\log_2^2x+6\log_2x+9=4\log_2x+4m+4\sqrt{\log_2x+m}+1\)
\(\Leftrightarrow\left(\log_2x+3\right)^2=\left(2\sqrt{\log_2x+m}+1\right)^2\)\(\Leftrightarrow\left[{}\begin{matrix}2\sqrt{\log_2x+m}+1=\log_2x+3\\2\sqrt{\log_2x+m}+1=-\log_2x-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2\sqrt{\log_2x+m}=\log_2x+2\left(1\right)\\2\sqrt{\log_2x+m}=-\log_2x-4\left(2\right)\end{matrix}\right.\)
Xét pt(1) <=> \(4\log_2x+4m=\log_2^2x+4\log_2x+4\Leftrightarrow\log_2^2x+4-4m=0\)
pt có nghiệm thì \(\Delta\ge0\Leftrightarrow-4\left(4-4m\right)\ge0\Leftrightarrow m\ge1\)
Xét pt(2) <=> \(4\log_2x+4m=\log_2^2x+8\log_2x+16\Leftrightarrow\log_2^2x+4\log_2x+16-4m=0\)
pt có nghiệm thì \(\Delta\ge0\Leftrightarrow4^2-4\left(16-4m\right)\ge0\Leftrightarrow m\ge3\)
Để pt đề bài có nghiệm thì ít nhất một trong hai pt (1) và (2) có nghiệm
Từ đề bài suy ra \(1\le m\le2023;m\in Z\) => m thuộc {1;2;....;2023} => Có 2023 giá trị m nguyên thỏa mãn