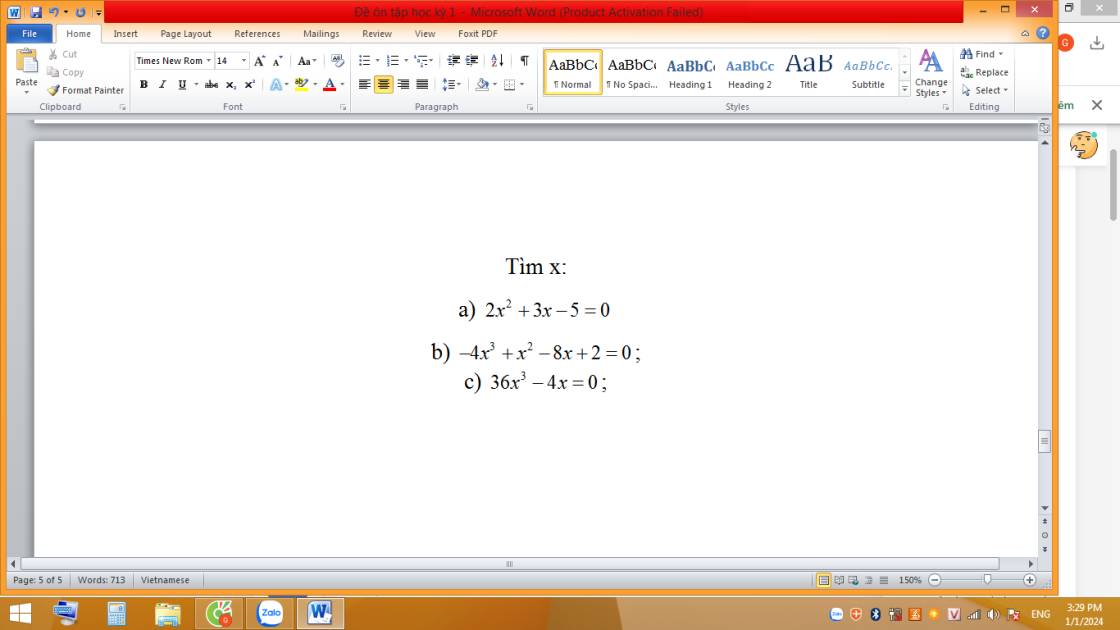
`a, 2x^2+3x-5=0`
`<=> 2x^2+5x-2x-5=0`
`<=> x(2x+5) -(2x+5)=0`
`<=> (2x+5)(x-1)=0`
\(\Leftrightarrow\left[{}\begin{matrix}2x+5=0\\x-1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}2x=-5\\x=1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{5}{2}\\x=1\end{matrix}\right.\)
`b,-4x^3+x^2-8x+2=0`
`<=>- x^2(4x-1)-(8x-2)=0`
`<=> -x^2(4x-1) -2(4x-1)=0`
`<=>(4x-1)(-x^2-2)=0`
\(\Leftrightarrow\left[{}\begin{matrix}4x-1=0\\-x^2-2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}4x=1\\-x^2=2\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{4}\\x\in\varnothing\end{matrix}\right.\)
`c, 36x^3-4x=0`
`<=>4x(9x^2-1)=0`
`<=>4x(3x-1)(3x+1)=0`
\(\Leftrightarrow\left[{}\begin{matrix}4x=0\\3x-1=0\\3x+1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\3x=1\\3x=-1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{3}\\x=-\dfrac{1}{3}\end{matrix}\right.\)